00. 들어가기 전에
문득 통계에서 분산과 표준편차를 구분해서 사용하는 이유가 궁금해졌습니다.
표준편차는 단순히 분산에 제곱근을 취한 것일 뿐인데, 왜 별개의 이름을 갖고 의미를 부여하였을까? (혹은 그 반대)
둘 모두 데이터가 퍼져있는 정도를 의미하고 각 통계량이 단독으로는 어떠한 정보를 전달하기 힘듭니다.
그런데 왜 굳이 분산과 표준편차라는 개념이 독립되어 사용하는지에 대한 의문이 생겨 이것저것 찾아보았습니다.
문제를 해결하는 과정에서 새롭게 드는 생각이 여럿 있었기 때문에, 여러 게시글에 걸쳐 정리해보려 합니다.
혹시 아래의 논리 전개가 적절하지 못하다고 생각하시는 분은 댓글을 통해 조언해주셨으면 합니다.
01. 분산을 구할 때 왜 편차를 제곱할까?
우선 분산과 표준편차를 구하는 방법 정도는 이미 알고 있을 거라고 가정하고 설명하겠습니다.
분산은 아래와 같은 식으로 구하는데 식을 보면 편차를 제곱한 후 데이터의 개수로 나누어주게 됩니다.

아래와 같이 편차를 그냥 더해버리면 편차의 평균이 0이 되어버릴 수도 있습니다.
분명 평균에서 떨어져 있는 값들인데 데이터가 퍼져있는 정도를 표현했더니 0이 되어버린다면 조금 이상합니다.

그렇다면 왜 편차의 절댓값은 사용하지 않을까요?
물론 절대편차라는 개념도 존재하지만 여기서는 일단 생각하지 않겠습니다.
절댓값을 이용해도 여전히 문제는 남아있습니다. 아래 그림을 보며 생각해보겠습니다.

첫 번째 경우와 두 번째 경우는 한 눈에 봐도 데이터가 퍼져있는 정도가 다릅니다.
그런데 절댓값을 사용하여 편차의 평균을 구하면 데이터가 퍼져있는 정도가 같다고 계산됩니다.
조금 더 극단적인 예시를 들어 \(\pm0.00001, \pm5.99999\) 같은 경우를 생각해보면 좀 더 와닿을 것 같습니다.
이런 경우에 대한 적절한 설명을 하기 위해서 편차를 제곱한 값을 통해 분산을 구하는 것입니다.
02. 그렇다면 왜 분산과 표준편차를 굳이 구분할까?
본격적으로 분산과 표준편차를 굳이 구분하는 이유에 대해서 알아보겠습니다.
보통 이에 대해 검색해보면 다음과 같은 설명이 일반적입니다.
분산은 편차를 제곱하였기 때문에 원래 데이터와 측정 단위가 다르다.
따라서 표준편차를 사용하여 단위를 맞춰주는 것이다.
맞는 이야기입니다. 표준편차와 분산은 당연히 단위가 다릅니다.
하지만 여전히 처음 가진 의문에 대한 명쾌한 답이라고 보기엔 조금 어렵습니다.
측정 단위가 달라서 측정 단위를 맞춰주는 것이 목적이라면 분산이라는 개념은 왜 남겨둘까요?
또 다른 설명은 다음과 같은데, 아마 이게 처음 의문에 대한 더 적절한 대답이 되지 않을까 싶습니다.
분산은 "평균"으로부터 각 데이터가 얼마나 멀리 떨어져 있는지를
표준편차는 "전체적"인 데이터의 분포를 알려준다.
단번에 의미를 파악하신 분들도 계시겠지만, 어떤 느낌인지 대충은 알겠지만 한 번에 와닿는 설명은 아닌 것 같습니다.
이해를 돕기 위해서 MSE와 RMSE의 예시를 들어서 한번 설명해보겠습니다.
MSE, RMSE는 딥러닝에서 흔히 사용되는 오차 함수입니다.
이름에서 알 수 있듯이 RMSE(Root Mean Squared Error)는 MSE(Mean Squared Error)에 제곱근을 취한 값입니다.
MSE는 편차인 \(\hat y - y \) 를 제곱하여 사용하기 때문에 이상치에 민감할 수밖에 없습니다.
즉, 일반적으로 정상적인 범주로 여기는 '평균'에 비해서 얼마나 비정상적인 값이 많은지를 직관적으로 알게 해줍니다.
반면 RMSE는 이상치에 덜 민감하지만 측정단위가 원래 데이터와 같기 때문에 전체적인 데이터의 분포를 알기 쉽습니다.
이런 차이점 때문에 분산과 표준편차의 개념을 특별히 구분하여 사용한다고 생각할 수 있습니다.
03. 표준편차는 왜 '표준' 편차일까?
사실 더 중요한 점은 표준편차(Standard Deviation)에 왜 "표준(Standard)"이라는 용어가 사용되었을까 입니다.
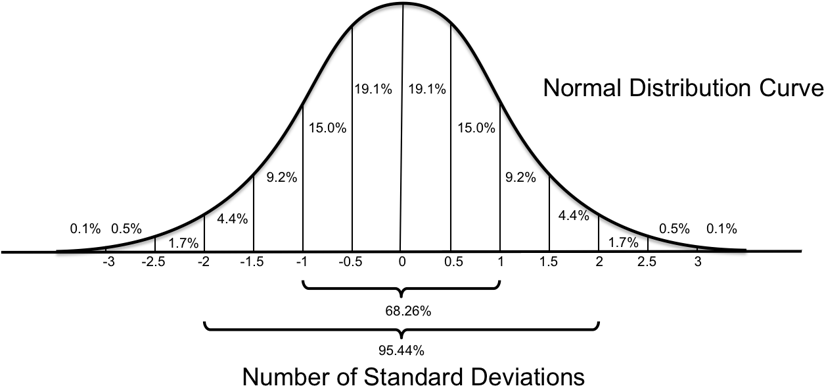
표준편차는 특정한 데이터 분포에서 어떤 값이 얼마나 자주 발생할지를 쉽게 알게 해줍니다.
여기서 특정한 데이터 분포는 정규분포(Normal Distribution)를 의미합니다.
예를 들어서 위 그림에서, 어떤 값이 평균보다 2 표준편차만큼 높은 경우
전체 데이터의 2.5%만이 이와 같이 극단적인 값을 가능성이 있다고 생각할 수 있습니다.
결국 표준편차를 기준으로 하여 어떤 값이 발생할 가능성을 알 수 있고, 이러한 이유로 '표준'편차라는 이름을 갖습니다.
참고로 여기서 데이터가 정규분포를 따라야 한다고 했는데, 중심극한정리에 의해 표본집단은 정규분포를 따르게 됩니다.
중심극한정리는 동일한 확률분포를 가진 확률변수들의 평균의 분포는 정규분포에 가까워진다는 내용입니다.
데이터 분석시 모든 데이터를 분석하기 어렵기 때문에 표본으로부터 모집단을 추정하는 개념과 관련된 내용인데,
이에 대한 내용은 표본분산에 대한 글을 작성하며 추후 조금 더 자세히 다뤄보겠습니다.
04. Reference
https://www.sv-europe.com/blog/whats-standard-about-a-standard-deviation/
https://keydifferences.com/difference-between-variance-and-standard-deviation.html
'Math Basic' 카테고리의 다른 글
| 딥러닝 논문의 수식을 LaTex로 작성하기 (1) | 2023.10.06 |
|---|

댓글