N그램 언어 모델

자연어 처리에서 언어 모델링은 문장의 일부가 주어졌을 때 이후에 나올 단어를 예측하는 과제를 말합니다. 현재는 딥러닝에 기반한 다양한 기술로 언어 모델을 설계하지만, 과거에는 통계적인 기법들을 사용한 통계적 언어 모델(statistical language mdoel)을 사용하였습니다. 사실 신경망 언어 모델(neural language model)도 훈련 목표만 놓고 보면 전통적인 언어 모델의 훈련 목표와 다르지 않습니다. 다만 각 단어를 표현하는 방법이나 모델이 목적 함수를 학습하는 방법에 차이가 있을 뿐입니다.

 

가장 대표적인 통계적 언어 모델 $N$ 그램입니다. $N$ 그램(N-gram)은 이전에 등장한 $N-1$ 개의 단어에 대하여 다음 단어를 예측하는 확률론적 모델입니다. 여기서 $N$그램은 $N$개의 토큰 시퀀스를 의미합니다. 토큰, 또는 단어의 개수에 따라 구체적으로는 유니그램(unigram), 바이그램(bigram), 트라이그램(trigram) 등으로 불립니다. 앞서 언급했듯이 이와 같은 단어 시퀀스의 통계적 모델을 언어 모델(language model) 또는 LM이라고 합니다.

 

$N$그램과 같이 이어질 수 있는 단어에 조건부 확률을 부여하는 추정기를 사용하여 전체 문장에 대한 결합 확률을 계산할 수 있습니다. $N$ 그램은 기계 번역(machine translation)에서도 흔히 사용되어 번역된 문장에서 문맥에 맞는 단어가 사용되도록 합니다. 또한 철자 수정(spelling correction)에서도 확률 추정기를 사용해 오류를 감지하고 수정을 제안할 수 있습니다. 장애인을 돕는 의사소통 보완(augmentative communication) 시스템에서도 단어 예측은 중요합니다. 음성이나 수화를 통해 의사소통을 할 수 없는 사람들은 간단한 신체 동작을 이용해 시스템이 말하는 메뉴에서 단어를 선택함으로써 의사소통을 할 수 있는데, 이 때 단어 예측을 사용해 적합한 단어를 제안할 수 있습니다.

 

---

 

Unsmoothed Ngram

$N$ 그램의 목표는 어떤 history $h$가 주어졌을 때 단어 $w$로 이어질 확률 $P(w|h)$를 계산하는 것입니다. 예를 들어 “its water is so transparent that”이라는 history가 주어졌을 때 다음 단어가 the일 확률을 알고 싶다고 가정하겠습니다.

 

 

이 확률은 어떻게 계산할까요? 한 가지 방법은 상대 빈도(relative frequency)를 세어서 추정하는 것입니다. 예를 들어서 매우 큰 말뭉치(corpus)에서 the water is so transparent that이 나타난 횟수를 세고, the가 이어지는 횟수를 셉니다. 이는 다음과 같이 표현할 수 있습니다.

 

 

이런 방식은 잘 작동할테지만, 엄청나게 큰 말뭉치가 있어야만 예측이 제대로 이루어질 것입니다. 그런데 언어는 독창적이기 때문에 새로운 문장은 계속해서 만들어지고, 이 모든 문장을 셀 수는 없습니다. 따라서 더 나은 방법이 필요합니다. 계속해서 수식적 표현을 사용해야 하기 때문에, 이에 앞서 표기를 조금 공식화하겠습니다. 앞으로는 임의의 확률 변수 $X_i$가 “the”를 취할 확률 $P(X_i=\textrm {the})$를 단순화하여 $P(the)$로 나타내겠습니다. $N$ 단어의 시퀀스 $w_1,\dots,w_n$은 $w_1^n$으로 나타냅니다. 그리고 어떤 값 $P(X=w_1, Y=w_2,Z=w_3,\dots,W=w_n)$을 갖는 시퀀스 내 각 단어의 결합 확률을 $P(w_1,w_2,\dots,w_n)$으로 나타냅니다.

 

그렇다면 전체 시퀀스의 확률을 어떻게 계산할 수 있을까요? 한 가지 방법은 다음과 같이 확률의 연쇄 법칙을 사용해 확률을 분해하는 것입니다.

 

 

마찬가지로 이 연쇄 법칙을 단어 시퀀스에 사용하면 다음과 같이 될 것입니다.

 

 

하지만 이 연쇄 법칙도 충분하지는 않습니다. 앞의 예시와 같이 긴 문자열 뒤에 단어가 나타나는 확률은 제대로 추정하기 어렵기 때문입니다. 실제로 its water is so transparent that 다음에 the가 나올 확률이나, its water is so 다음에 transparent가 나올 확률을 추정하는 건 둘 다 쉬운 일이 아닙니다.

 

따라서 $N$ 그램 모델은 전체 history를 마지막 몇 단어에 대한 history로 근사하여 나타냅니다. 예를 들어 bigram 모델은 이전 단어에 대한 조건부 확률 $P(w_n|w_{n-1})$만을 사용해 $P(w_n|w_1^{n-1})$을 근사합니다. 수식으로 나타내면 다음과 같습니다.

 

 

이처럼 단어의 확률이 바로 이전의 단어 하나에 의존한다는 가정을 마르코프(Markov) 가정이라고 한합니다. 이를 일반화하면 $N$그램을 생각할 수 있습니다.

 

 

bigram 모델에서는 전체 문장의 확률은 다음과 같이 표현할 수 있습니다.

 

 

그렇다면 이러한 bigram 또는 $N$그램의 확률은 어떻게 추정할까요? 확률을 추정하는 단순하고 직관적인 방식으로 최대 우도 추정법, MLE(Maximum Likelihood Estimation)가 있습니다. MLE에서는 말뭉치에서 $n$-gram 카운트를 계산하여 모델의 MLE 파라미터를 추정하고 이 값을 0과 1사이로 정규화한다. 설명만 봐서는 이해하기 어려우니 예시를 통해 알아보겠습니다.

 

예를 들어 이전 단어 $x$가 주어졌을 때 어떤 단어 $y$가 나타날 바이그램 확률을 계산하기 위해 먼저 바이그램 카운트 $C(xy)$를 구하고 단어 $x$로 시작하는 모든 바이그램의 개수로 나누어 정규화합니다.

 

 

그런데 이 식의 분모에서 결국 이전 단어 $w_{n-1}$로 시작하는 모든 bigram의 개수와 단어 $w_{n-1}$의 unigram 개수는 같아야 한다는 것을 알 수 있습니다. 따라서 식을 다음과 같이 단순화할 수 있습니다.

 

 

이 식을 다시 $N$그램으로 확장하면 다음과 같이 쓸 수 있습니다.

 

 

위 수식의 우변과 같이 어떤 시퀀스의 관측 횟수(count)를 접두사(prefix)의 관측 횟수로 나는 것을 상대 빈도(relative frequency)라고 합니다. 이처럼 상대 빈도를 통해 확률을 추정하는 과정이 바로 MLE의 한 예라고 볼 수 있습니다. 즉 MLE에서는 모델 $M$에게 주어진 학습 데이터셋 $T$에 대한 확률, 즉 $P(T|M)$을 최대화합니다.

 

---

 

Perplexity

언어 모델의 성능을 평가하는 방법 중 하나는 언어 모델을 어떤 어플리케이션에 포함하고 해당 어플리케이션의 전체 성능을 측정하는 것입니다. 이런 평가를 외재적 평가(extrinsic evaluation)이라고 하며 조건 내(in vivo) 평가라고도 합니다. 하지만 외재적 평가는 경제적이지 않기 때문에, 언어 모델의 잠재적인 성능을 빠르게 평가할 수 있는 측정 지표가 필요합니다. 내재적 평가(intrinsic evaluation) 지표는 적용 사례에 관계없이 모델의 품질을 측정합니다. 복잡도(Perplexity)는 N 그램 언어 모델에 대한 가장 기본적인 평가 지표입니다.

 

어떤 테스트 데이터셋이 주어졌을 때 언어 모델의 Perplexity는 테스트 세트에 할당하는 확률에 대한 함수입니다. 예를 들어 테스트 세트 $W=w_1w_2\dots w_N$의 복잡도는 다음과 같이 계산합니다.

 

 

이 식에 연쇄 법칙을 사용하면 다음과 같이 나타낼 수 있습니다.

 

 

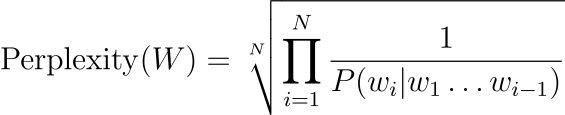
따라서 테스트 세트 $W$의 복잡도를 bigram 언어 모델에서 계산하면 식이 다음과 같이 단순해집니다.

 

 

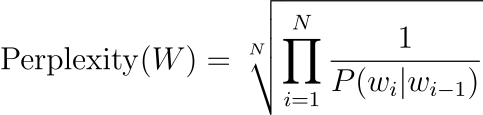
모든 확률은 0에서 1 사이의 값을 갖고, 곱해진 확률 값도 마찬가지로 같은 범위 내에 존재합니다. 이 값에 $-{1\over N}$ 제곱이 취해지면 다음과 같이 확률이 커질수록 결과값은 감소합니다. 따라서 확률이 크다는 것은 MLE에서 조건부 확률 추정이 잘 되었다는 의미이므로 Perplexity가 낮을수록 언어모델의 성능이 좋다고 생각할 수 있습니다.

 

 

---

 

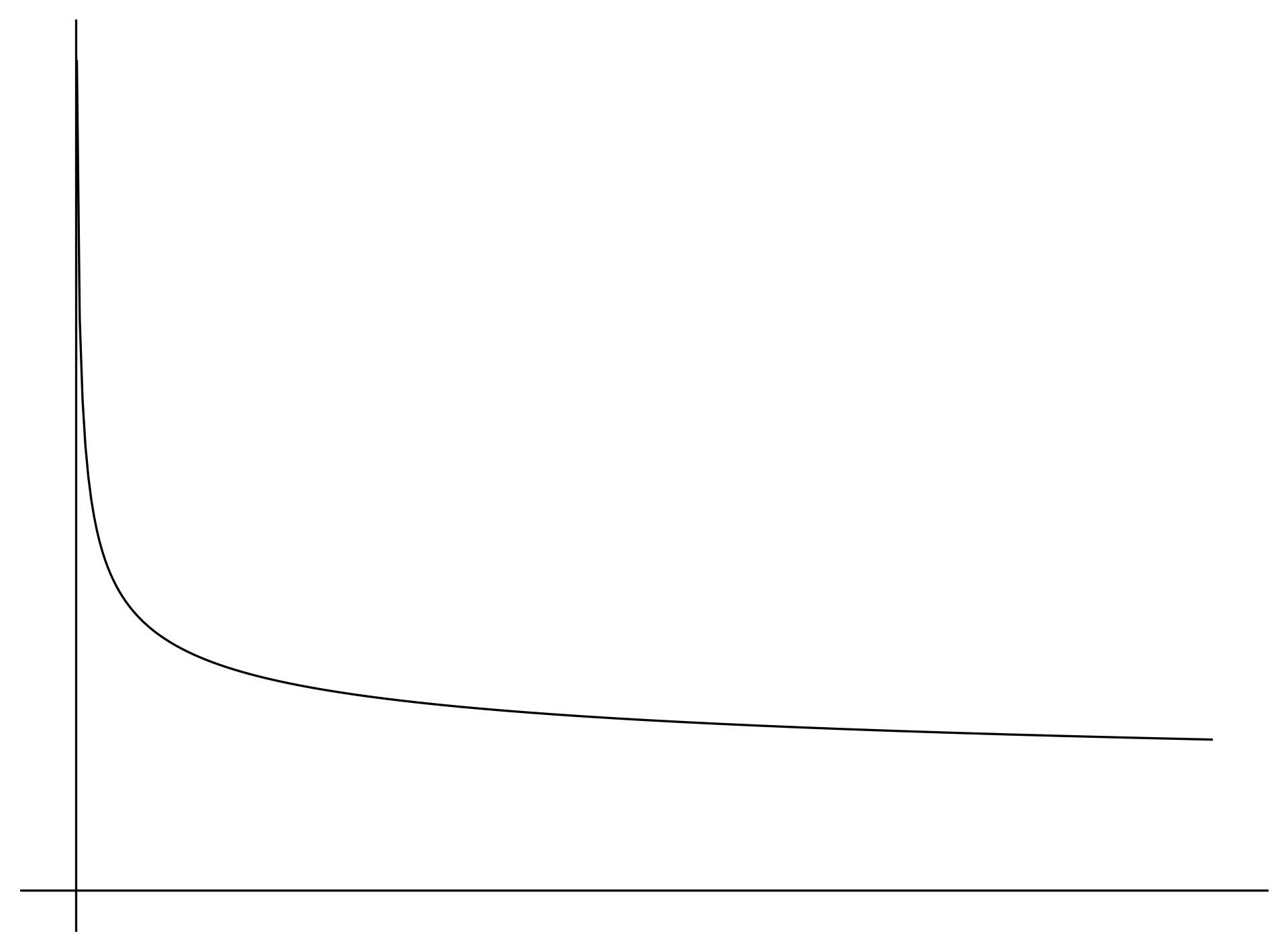
합리적인 근사를 통해 다음 단어를 예측하는 통계적 언어 모델인 N그램을 설계할 수 있었지만, 이 모델은 부족한 점이 아직 많이 남아있습니다. 여전히 학습 과정에서 한 번도 보지 못한 시퀀스에 대한 확률은 추정할 수 없기 때문에, 테스트 과정에서 새로운 문장을 만나게 되면 합리적인 문장이라도 0이라는 확률을 부여할 것입니다. 물론 통계적 언어 모델은 신경망 기반 모델보다 이런 확률을 정교하게 설계하기가 어렵지만, 그래도 이런 문제를 부분적으로나마 해소하기 위한 방법이 몇가지 있습니다. 이후에는 이런 기법 중 일부인 smoothing에 대해서 정리해보겠습니다.