
신경망에 기반한 언어 모델링이라는 새로운 패러다임을 제시한, NLP에서 정말 중요하고 획기적인 논문인 A Neural Probabilistic Language Model을 리뷰해보았습니다. 이 글은 논문의 전반부를 다룬 이전 글에서 이어집니다. 여기서는 실험 결과와 결론까지의 Section을 다룹니다. 번역을 통해 오히려 이해가 어려워지거나, 원문의 표현을 사용하는 게 원래 의미를 온전히 잘 전달할 것이라고 생각하는 표현은 원문의 표기를 따랐습니다. 오개념이나 오탈자가 있다면 댓글로 지적해주세요. 설명이 부족한 부분에 대해서도 말씀해주시면 본문을 수정하겠습니다.
4. Experimental Results
비교 실험은 영어 텍스트와 책에서 가져온 약 180만 개의 단어로 된 Brown 말뭉치로 수행되었습니다. 첫 80만 개의 단어는 학습에 사용되었고, 20만개는 검증에 나머지 18만개는 테스트에 사용되었습니다. 3번 이하로 등장한 희귀한 단어는 하나의 기호로 대체하여 총 47,578개의 단어에서 16,383개의 단어만을 어휘사전에 포함하였습니다.
또 다른 데이터인 Associated Press(AP) 뉴스에 대한 실험도 수행되었습니다. 140만 개의 단어로 이루어진 학습 데이터, 약 100만 개의 단어로 이루어진 검증 데이터와 테스트 데이터를 사용하였습니다. 원래 데이터는 148,272개의 서로 다른 단어를 가지는데, |V|=17964로 줄였습니다.
학습에 사용한 학습률은 ϵ0=10−3이고 학습 스케줄러 ϵt=ϵ01+rt에 의해 학습률이 점차적으로 감소하도록 하였습니다. 여기서 t는 업데이트가 완료된 파라미터의 개수이며 r=10−8의 decrease factor입니다.
4.1 N-Gram Models
신경망 모델과 비교한 첫 번째 벤치마크는 interpolated 또는 smoothed trigram model입니다. qt=l(freq(wt−1,wt−2))가 입력 context (wt−1,wt−2)의 이산화된 출현 빈도를 나타낸다고 하겠습니다. 그러면 조건부 확률은 다음과 같이 conditional mixture의 형태로 나타납니다.

Conditional weights \boldsymbol\alpha_i(q_t) \ge 0,\sum_i \boldsymbol\alpha_i(q_t)=1입니다. 여기서 p_0=1/|V|이고, p_1(i)부터 p_3(i|j,k)는 순서대로 unigram, bigram, trigram을 의미합니다. (w_{t-1}, w_{t-2})의 빈도가 크면 p_3에 가장 많이 의존하고, 낮으면 더 낮은 차수인 p_2, p_1 또는 p_0에 더 많이 의존합니다. Context frequency bins인 q_t의 각 이산 변수에 대해 서로 다른 mixture weights 집합 \alpha가 있습니다.
여기서 context frequency bins는 n-gram 언어 모델링에서 많은 수의 가능한 단어 시퀀스를 처리하기 위해 사용되는 기법입니다. 각각의 고유한 n-gram을 모두 별개로 보지 않고 유사한 context는 발생 빈도에 따라 bin으로 그룹화합니다. 빈도에 따라 context를 묶으면 통계적 스무딩 기법을 적용하여 빈도가 낮은 n-gram에 대한 확률을 추정할 수 있습니다. 이렇게 하면 유사한 context의 정보를 모아서 모델은 희귀한 시퀀스에 대해 더 많은 정보를 바탕으로 예측이 가능합니다. 또한 그룹화를 하면 모델이 계산해야 할 파라미터의 수도 줄어듭니다.
이어서, 가중치는 EM 알고리즘을 사용하여 쉽게 추정할 수 있습니다. Interpolated n-gram은 여러가지 오류를 유발했기 때문에 MLP와 함께 사용되었습니다.
또한 또 다른 SOTA n-gram 모델인 back-off n-gram, class-based n-gram 모델과의 비교도 수행되었습니다. 검증 세트는 class-based 모델의 단어 클래스의 개수와 n-gram의 순서를 선택하는 데 사용되었습니다.
4.2 Results
서로 다른 모델 \hat P의 테스트 세트에서의 perplexity를 측정하였습니다. Brown 말뭉치에 대해서는 10에서 20 에포크를 학습한 후 stochastic gradient ascent가 수렴하였습니다. AP News는 5 에포크만을 실행하였기 때문에 과대적합이 일어나지 않았습니다. 검증 세트에 대해 조기 종료가 사용되었지만 Brown 데이터를 사용한 실험에서만 필요했습니다. Brown과 AP News 각각에서 weight decay는 10^{-4}와 10^{-5}가 사용되었습니다. 다음 표는 Brown 말뭉치에 대한 실험 결과입니다. 모든 back-off 모델은 더 뛰어난 성능을 보이는 Kneser-Nay n-grams으로 대체되었습니다. Back-off 모델에서 m이 특정될 경우, class based n-gram 모델이 사용되었습니다. 단어의 특성 벡터는 임의로 초기화되었지만, 사전 지식에 기반하여 초기화했다면 더 나은 결과를 얻을 것이라고 추정하였습니다.
주요 결과는 신경망을 사용할 경우 n-gram 모델에 비해 눈에 띄게 성능이 향상된다는 것입니다. 표에서는 신경망을 사용할 경우 더 많은 문맥을 사용할 때 이점을 얻을 수 있다는 것도 알 수 있습니다. 예를 들어 Brown 데이터에서, 2 단어의 context보다 4단어를 사용할 때 신경망에서는 성능이 향상되었지만, n-gram에서는 그렇지 않았습니다. 또한 hidden unit을 사용하는 것이 유용하며 interpolated trigram과 신경망의 출력을 함께 사용하면 perplexity를 줄이는 데 도움이 되었습니다. 단순히 평균을 내는 것이 도움이 되었다는 점에서 신경망과 trigram 모델이 서로 다른 곳에서 문제를 일으키고 있음을 알 수 있습니다.

표에서 n은 모델의 order(예측 과정에서 몇 개의 단어가 고려되었는지), c는 class-based n-grams에서 word classes의 개수, h는 hidden unit의 개수, m는 MLP에서 word features의 개수, direct는 word features과 output 사이에 직접적인 연결이 있었는지, mix는 신경망의 출력 확률이 trigram의 출력과 함께 사용되었는지(가중치의 0.5씩)을 의미합니다. 마지막 세 개의 열은 각 단계에서의 perplexity를 의미합니다.
아래 표는 더 큰 말뭉치인 AP New에 대한 실험결과입니다. 5 에포크만을 학습한 후 비교했기 때문에 perplexity의 차이가 이전처럼 크지는 않았습니다.

5. Extensions and Future Work
5.1 An Energy Minimization Network
실험에서 사용한 다양한 신경망 모델은 energy minimization mopdel로 해석될 수 있습니다. Distributed word features는 출력 단어(다음 단어)가 아닌 입력 단어에 대해서만 사용됩니다. 게다가 매우 많은 수의 파라미터는 출력 레이어에 존재하여 출력 단어들의 의미적, 구조적 유사도는 고려되지 않습니다. 여기서 묘사하는 변형은 출력 단어 또한 특성 벡터로 표현됩니다. 네트워크는 특성 벡터로 매핑된 단어들의 sub-sequence를 입력으로 받아 에너지 함수 E를 출력합니다. 그럴듯한 sub-sequence를 생성하면 그 값이 작고 그렇지 않으면 값이 커집니다. 에너지 함수는 다음과 같습니다.
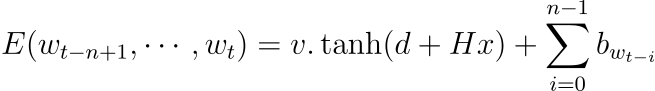
b는 편향의 벡터이며 d는 hidden unit bias의 벡터, v는 출력 가중치 벡터, H는 히든 레이어의 가중치 행렬을 의미합니다. 그리고 이전 모델과 다르게 입력과 출력 단어는 x에 다음과 같이 영향을 미칩니다.
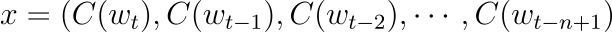
에너지 함수는 (w_{t-n+1}, \cdots,w_t)가 함께 나타(joint occurence)날 때에 대한 정규화되지 않은 로그 확률(unnormalized log-probability)로 해석될 수 있습니다. 조건부 확률 \hat P(w_t|w_{t-n+1}^{t-1})를 얻기 위해 가능한 w_t의 값에 대해 다음과 같이 정규화될 수 있습니다.
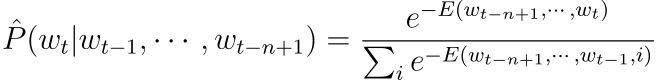
총 연산량은 이전의 아키텍처와 크게 다르지 않고 v 파라미터가 타겟 단어 w_t에 의해 결정된다면 파라미터의 개수 또한 같습니다. 전체 시퀀스에 대한 확률을 각 원소에 대한 조건부 확률로 분해하였기 때문에, 그라디언트를 계산하는 것은 쉽습니다. 이를 바탕으로 구현한 아키텍처에서 실험을 진행하였고, 신경망 학습을 빠르게 하는 기술을 개발할 수 있었습니다.
Out-of-vocabulary words
이전에 비해 이 아키텍처가 갖는 장점은 사전에 없는 단어(out-of-vocabulary words, oov)를 쉽게 다룰 수 있다는 것입니다. 먼저 같은 문맥에 등장하는 다른 단어들의 특성 벡터들의 weighted convex combination을 취하여 oov 단어의 특성 벡터를 초기화합니다. 예를 들어 문맥 w_{t-n+1}^{t-1} 내부의 단어 i\in V에 확률 \hat P(i|w_{t-n+1}^{t-1})을 할당했다고 가정하고 이 문맥 안에서 새로운 단어 j \notin V를 관측했다고 하겠습니다. 그러면 특성 벡터 C(j)는 C(j) \leftarrow\sum_{i\in V}C(i)\hat P(i|w_{t-n+1}^{t-1})로 초기화됩니다. 그러면 j를 V에 포함하여 아주 약간 커진 집합에 대해 확률을 다시 계산합니다. 이는 i를 제외한 모든 단어에 대한 renormalization 연산만을 필요로 합니다. 이 특성 벡터 C(i)는 i 다음에 오는 단어의 확률을 예측할 때 input context part로 사용될 수 있습니다.
5.2 Other Future Work
저자는 연구 내용에 대하여 추가적으로 해결해야 할 과제가 많다고 하였습니다. 단기적으로는 설계와 검증을 위해서 학습과 인지(recognition)을 빠르게 하는 방법이 필요하다고 하였습니다. 그리고 장기적으로는 이 논문에서 제안한 두 가지 방법(distributed representations, neural network modeling) 외에 일반화를 위한 더 많은 방법이 도입되어야 한다고 하였습니다. 그러면서 추가로 연구되어야 할 몇 가지 아이디어를 제시합니다.
- 단어의 클러스터를 사용하는 등 신경망을 sub-networks로 분해합니다. 이렇게 하면 학습이 더 쉽고 빠르게 이루어집니다.
- 조건부 확률을 트리 구조로 표현하여 신경망이 각 노드에 적용되게 합니다. 각 노드는 문맥이 주어졌을 때 단어 클래스의 확률을 나타내고 잎은 문맥이 주어졌을때 단어들의 확률을 나타냅니다. 이런 표현은 연산량을 |V|/log|V|에 비례하게 줄일 수 있습니다.
- 출력 단어의 부분 집합에만 그라디언트를 전파합니다. 이 부분 집합은 조건적으로 가장 그럴듯한 단어들일 수도 있고, trigram의 성능이 좋지 못한 단어의 부분집합일 수도 있습니다.
- 사전 지식(priori-knowledge)를 사용합니다. 이러한 사전 지식에는 WordNet이나 Fellbaum으로부터 의미 정보, 형태소를 사용한 저수준의 문법 정보, stochastic grammar을 사용하는 고수준 문법 정보 등이 있습니다. time-delay나 순환 신경망을 사용하는 등 더 많은 모델 구조나 파라미터가 공유되면 더 긴 문맥을 효과적으로 포착할 수 있을 것입니다.
- 신경망을 통해 학습한 단어의 특성 벡터를 해석합니다. 간단한 방법은 m=2일 때로 시작해보는 것입니다. 이렇게 하면 시각화를 하기도 편합니다. 저자는 m이 커지면 의미 있는 정보를 학습하기 위해서 더 많은 학습 데이터가 필요하다고 하였습니다.
- 논문의 모델은 각 단어에 연속 의미 공간에서 하나의 점만을 할당하기 때문에 다의어(polysemous words)를 잘 처리하지 못할 것입니다. 저자는 모델을 확장하여 각 단어를 공간 내의 여러 점에 연관짓는 연구를 수행하고자 하였습니다.
6. Conclusion
두 말뭉치에서 실험한 제안된 접근법이 기존의 SOTA 모델보다 perplexity 면에서 훨씬 나은 성능을 보임을 입증하였습니다. 주요 원인은 학습된 분산 표현이 차원의 저주 문제를 해결하는 데 큰 이점을 갖기 때문이라고 하였습니다. 이를 통해 학습에 사용한 문장은 다른 수많은 문장들에 대한 정보를 모델에게 제공할 수 있습니다.
저자는 모델을 한층 더 발전시키기 위하여, 아키텍처, 연산 효율성, 사전 지식의 이점을 활용하는 측면에서 여전히 많은 가능성을 갖고 있다고 하였습니다. 그러면서 학습 시간을 너무 많이 증가시키지 않으면서 한 번에 더 많은 데이터를 학습하는 방법과 더불어 speed-up technique의 발전을 우선순위로 두었습니다. 또한 그 방법 중 하나로 time-delay나 순환 신경망 사용할 수 있을 것이라고 하였습니다.
보다 일반적으로 논문의 연구는 통계적 언어 모델을 개선하기 위한 시작점이 됩니다. 이는 더 많은 conditioning variables 를 수용할 수 있는, 분산 표현에 기반한 tables of conditional probabilities 덕분입니다. 통계적 언어 모델에서 과대적합을 방지하기 위해 conditioning variables를 제한하거나 줄이려는 노력이 정말 많이 들어갔지만, 여기서 제안한 모델은 그 어려움을 다른 문제로 바꿨습니다. 더 많은 연산이 필요하다는 것인데, 연산과 메모리 요구량은 지수적으로 증가하는 conditioning variables와 다르게 선형적으로 증가합니다.
7. Further Thinking
현재까지 읽은 논문 중에 제일 어렵고 호흡이 길었습니다. 하지만 그만큼 NLP와 단어 임베딩에서 중요하게 여겨지는 논문이기에 나름 집중해서 끝까지 마무리한 것 같습니다. 여전히 완벽히 이해가 안되는 부분이 남아있습니다. 논문은 단순히 분산 표현, 즉 단어 임베딩이라는 새롭고 혁신적인 개념을 제안한 것 뿐만 아니라, 언어 모델링의 패러다임 전환을 이끌면서 이에 따라 발생할 수 있는 여러가지 일들에 대해 폭넓게 다룹니다. 보통 이 논문에서 가장 주요하게 다루는 두 가지 개념을 꼽자면 분산 표현과 신경망을 통한 언어 모델링을 생각할 것입니다. 그런데 분산 표현은 결국 어떤 단어를 나타내는 특성 벡터를 의미하고, 이 특성 벡터가 갖는 값을 결정하기 위한 수단이 신경망이라는 것을 생각하면 둘은 결국 뗄 수 없는 개념입니다. 특성 벡터의 가중치를 결정하기 위해 정말 많은 연산량이 필요할텐데, 저자는 이 또한 염두에 두고 있었습니다.
호흡이 길고 깊이도 깊으며, 이해하기도 쉽지 않은 내용이었지만, 그 사이에 논리적 흐름이 매우 자연스럽고 탄탄해서 상당히 놀라웠습니다. 그리고 논문이 2003년에 발표되었다는 것을 감안할 때, 저자가 후속 연구로 제시한 주제들을 보고 또 한번 감탄했습니다. 신경망을 사용한 언어 모델링이 성공적으로 이루어지기 위하여 해결되어야 할 과제들을 정확하게 짚고 있고, 실제로 그런 주제들이 연구되어 지금의 언어 모델이 탄생했다고 생각합니다. 예를 들어 다의어를 여러 개의 점에 대응하는 것이 결국 contextualized representations이고, 특성 벡터를 해석하려는 시도도 결국 딥러닝 모델이 블랙박스라는 문제를 해결하기 위한 노력이라고 생각했습니다. 미래를 내다보는 저자의 통찰이 정말 놀라웠고, 왜 요슈아 벤지오 교수님께서 딥러닝계의 4대 석학이라고 여겨지는지를 다시 한 번 깨닫게 되었습니다.




댓글