
신경망에 기반한 언어 모델링이라는 새로운 패러다임을 제시한, NLP에서 정말 중요하고 획기적인 논문인 A Neural Probabilistic Language Model을 리뷰해보았습니다. 저자도 딥러닝의 4대 석학이라 불리는 요슈아 벤지오 교수님입니다. 이 논문은 단순히 출력 시퀀스에서 다음 단어를 예측하는 것을 넘어서 단어의 본질적인 의미를 포착하는 밀집 벡터 표현인 단어 임베딩의 시대를 열었다고 봐도 될 것 같습니다. 단어를 단순히 기호로 보는 것이 아닌 연속적인 공간에 매핑하는 임베딩은 NLP에서 단어와 그들의 관계에 대해 생각하는 방식에 혁명을 일으켰습니다. 이번 논문은 제안된 방법론 외에도 병렬화나 관련 이론에 대한 내용을 많이 포함하고 있어 두 부분으로 나누어 정리하였습니다. 여기서는 논문의 Section 3까지를 다룹니다. 번역을 통해 오히려 이해가 어려워지거나, 원문의 표현을 사용하는 게 원래 의미를 온전히 잘 전달할 것이라고 생각하는 표현은 원문의 표기를 따랐습니다. 오개념이나 오탈자가 있다면 댓글로 지적해주세요. 설명이 부족한 부분에 대해서도 말씀해주시면 본문을 수정하겠습니다.
Overview
언어 모델링을 어렵게 하는 근본적인 원인은 차원의 저주(curse of dimensionality)입니다. 특히 문장 내에 존재하는 단어들, 데이터 마이닝 작업에서의 여러 특성들과 같이 다양한 이산확률변수(discrete random variables)의 결합 확률 분포(joint distribution)를 모델링할 때 이 문제가 두드러집니다. 사전의 크기 V가 100,000일 때, 10개의 연속되는 단어에 대한 결합 확률 분포를 모델링하기 위해서는 10000010−1=1050−1개의 파라미터를 고려해야 합니다. 반면에 연속 변수를 모델링할 때는, 학습되는 함수가 local smoothness를 가질 것이기 때문에 일반화가 조금 더 쉽습니다.
여기서 local smoothness는 입력값이 서로 비슷하면, 결과도 비슷한 양상을 보이는 것을 말합니다. 이 개념이 논문의 핵심인데, 결국 각 단어를 독립적인 기호로 보는 것이 아니라 연속 변수, 즉 distributed representation으로 생각하겠다는 것입니다. 이렇게 하면 단어의 의미를 일반화할 수 있고, 학습 과정에서 보지 못했던 단어에 대해서도 어느 정도 이해가 가능합니다. 이어서 논문에서는 어떻게 설명하는지 설명하겠습니다.
이산 공간에서는 일반화 구조(generalization structure)이 연속 공간처럼 뚜렷하지 않습니다. 이산 변수의 변화는 추정하고자 하는 함수의 값에 큰 영향을 미치고, 각 이산 변수가 취할 수 있는 값이 많다면 대부분의 관측 대상은 가능한 멀리 떨어져 있는 경우가 많습니다.
다양한 학습 알고리즘이 어떻게 일반화되는지 시각화하는 유용한 방법은 non-parametric density estimation에 영감을 받았는데, 학습 문장과 같은 처음에 training points에 대해서 밀집되어 있는 확률 질량이 더 큰 공간에서는 어떻게 분포되는지를 생각하는 것입니다.
여기서 언급한 밀도 추정(density estimation)에는 크게 parametric과 non-parametric의 두 가지 방법이 있습니다. Parametric은 미리 확률 밀도 함수(probability density function, PDF)를 모델링하고 유의미한 통계치를 계산합니다. 그런데 현실의 문제에서는 모델을 비리 정할 수 없는 경우가 많기 때문에 순수하게 관측한 데이터만으로 PDF를 추정해야 합니다. 이를 non-parametric density estimation이라고 부르고, 흔히 히스토그램을 사용합니다. 예를 들어 관측된 데이터를 히스토그램을 통하여 나타내고 이를 정규화하여 PDF로 사용하는 것입니다.

높은 차원에서는 각 학습 데이터를 중심으로 모든 방향으로 균일하게 분포하는 것보다 핵심적인 방향으로 확률 질량을 분배하는 것이 중요합니다. 논문에서는 기존의 확률적 언어 모델링에 기반한 SOTA 모델과는 근본적으로 다른 이 언어 모델링 기법이 어떻게 잘 일반화되는지를 소개하였습니다.
통계적 언어 모델링은 다음 수식과 같이 이전 단어들이 주어졌을 때, 다음에 올 단어를 조건부 확률로 표현합니다.

wt는 t번째 단어이고 wji=(wi,wi+1,…,wj−1,wj)입니다. 이런 통계적 언어 모델은 자연어 처리, 음성 인식, 번역, 정보 검색 등 많은 기술적인 응용 사례에서 유용함이 이미 알려져 있습니다. 따라서 이를 발전시키면 해당 응용 사례에서도 성능이 향상될 것입니다.
자연어에 대한 통계 모델을 만들 때는, 문장 내에서 서로 가까이 위치한 단어끼리는 통계적으로 더 의존적일 것이라는 점에서 단어의 순서를 사용하면 난이도를 크게 낮출 수 있습니다. 따라서 다음과 같이 n-gram 모델은 거대한 문맥 안에서 n−1개의 이전 단어에 대하여 다음 단어의 조건부 확률을 고려합니다.

저자는 연속적인 단어의 조합에서 학습 데이터에 실제로 나타나는 경우만을 고려하였습니다. 그렇다면 이전에는 본 적이 없는 n개의 단어에 대한 새로운 조합이 발견되면 어떻게 할까요? 그런 경우에 대해서 항상 확률을 0이라고 생각할 수는 없습니다. 간단한 방법은 back-off trigram 모델에서처럼 더 작은 문맥에 대해서 생각하는 것입니다. 그런 모델에서는 새로운 경우에 어떻게 일반화가 이루어질까요? 새로운 단어의 시퀀스는 길이가 1, 2 또는 최대 n개의 단어로 이루어진 학습 데이터에서 자주 등장한 경우들을 이어붙이는(gluing) 식으로 생성합니다. 통상적으로는 n=3, 즉 trigram을 사용하였고, SOTA 모델이 될 수 있었습니다. 분명히 예측할 단어 바로 이전에 오는 단어가 이전의 여러 개의 단어보다 많은 정보를 가질 것입니다.
이런 방식에는 두 가지 개선할 점이 있고, 논문에서는 바로 이 점에 초점을 맞춥니다. 두 가지 개선점 중 첫 번째는 문맥을 고려할 때 1개 또는 2개 보다 더 멀리 떨어져 있는 단어는 생각하지 않는다는 것입니다. 두 번째는 단어 사이의 유사도를 고려하지 않는다는 것입니다. 이전에도 이런 문제를 해결하기 위한 여러 방법이 제안되었는데, 이에 대해서는 이후에 다루겠습니다.
논문에서 v는 열벡터를 의미하고 v′는 전치, 즉 행벡터를 의미합니다. Aj는 행렬 A의 j번째 행을, x.y=x′y를 의비합니다.
1.1 Fightning the Curse of Dimensionality with Distributed Representations
제안된 방법은 다음과 같이 요약할 수 있습니다.
- 어휘 사전 내의의 각 단어를 Rm 공간 내의 실수 벡터인 distributed word feature vector와 연관짓습니다.
- 단어 시퀀스의 결합 확률 분포 함수를 각 단어의 feature vectors로 표현합니다.
- word feature vectors와 확률 함수의 파라미터를 동시에 학습합니다.
특성 벡터(feature vector)는 단어의 서로 다른 측면을 표현합니다. 각 단어는 벡터 공간의 한 점과 관련이 있습니다. 특성의 수는 어휘사전의 크기에 비하면 매우 작습니다. 확률 함수는 이전 단어들이 주어졌을 때 다음 단어의 조건부 확률의 곱으로 표현합니다. 이 함수는 학습 데이터에 대하여 로그 가능도가 최대가 되도록 조정됩니다. 특성 벡터는 학습에 의해 결정되지만, 의미적 특성에 대한 사전 지식을 바탕으로 초기화될 수도 있습니다.
이렇게 하면 조금 전에 봤던 예시에서 dog과 cat이 의미적, 구조적으로 비슷한 역할을 수행하고 (the, a), (bedroom, room), (is, was), (running, walking)도 마찬가지라는 점에서 The cat is walking in the bedroom을 A dog was running in a room, The dog was walking in the bedroom 등의 문장에 자연스럽게 일반화할 수 있습니다. 제안된 모델에서 비슷한 단어는 비슷한 특성 벡터를 가질 것이고, 확률 함수는 이러한 특성값들의 smooth function이기 때문에 작은 변화는 확률에도 큰 영향을 미치지 않을 것이기 때문에 일반화가 가능합니다. 따라서 위 예시에서 첫 번째 문장만이 학습 데이터에 나타나더라도 이웃하는 여러 문장들의 확률 또한 따라서 증가할 것입니다.
1.2 Relation to Previous Work
신경망을 사용하여 고차원의 이산적인 분포를 모델링하는 아이디어가 확률 변수의 집합 Z1,…,Zn의 결합 확률을 학습하는데 유용하다는 것은 이미 밝혀져 있습니다. 해당 모델에서 결합 확률은 다음과 같이 조건부 확률이 곱으로 분해될 수 있습니다.
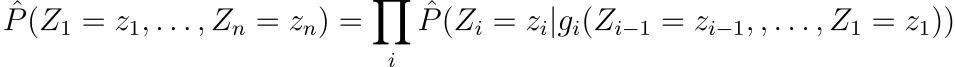
g(.)는 특별한 left-to-right 아키텍처를 갖는 신경망으로 표현되는 함수이며, i번째 출력 블럭 gi()는 이전의 Z 값들이 주어졌을 때 Zi의 조건부 분포를 표현하기 위한 파라미터를 계산합니다. UCI 데이터셋에을 활용한 실험에서 이 방법이 유용함이 검증되었습니다. 여기서 문장과 같이 일정하지 않은 길이이 데이터를 다루어야 하기 때문에 위와 같은 방법이 필요합니다. 여기서 중요한 차이점은 모든 i번째에 위치한 단어인 Zi 단어라는 같은 형식의 객체를 가리킵니다. 따라서 제안된 모델은 타임스템에 관계없이 파라미터를 공유할 수 있으며, 이는 같은 gi가 계속해서 사용될 수 있음을 의미하고 결국 서로 다른 위치에 있는 입력 단어에 대해서도 마찬가지입니다.
언어 모델링에 신경망을 사용하는 것도 아예 새로운 것은 아닙니다. 하지만 여기서는 그 규모를 확장하였고, 문장 내에서 단어가 수행하는 역할보다는 단어 시퀀스 분포의 통계적 모델을 학습하는 것에 초점을 맞추었습니다. 이 연구는 신경망을 사용하여 글자 기반으로 텍스트를 압축하고 다음 단어의 확률을 예측하는 과거 연구와도 연관되어 있습니다.
일반화를 위하여 단어의 유사도를 사용한다는 아이디어도 단어의 클러스터를 학습하는 과거 연구와 관련이 있습니다. 하지만 논문의 모델은 이산 확률 또는 결정적 변수를 사용하여 유사도를 계산하는 것이 아니라 연속적인 실수로 이루어진 벡터를 사용합니다. 따라서 learned distribution feature vector로 단어 사이의 유사도를 나타냅니다.
단어를 벡터 공간에 나타내는 것은 정보 검색 분야에서 사용되곤 합니다. 여기서는 단어의 특성 벡터가 같은 문서 내에서 함께 등장(co-occurence)하는 확률에 기반하여 학습됩니다. 중요한 차이점은 논문에서는 자연어 텍스트로부터 단어 시퀀스의 확률 분포를 간결하게 표현하는 데 도움이 되는 벡터 표현을 찾는다는 것입니다.
2. Neural Model
유한한 크기를 갖는 어휘 집합 V에 속하는 단어 wt∈V으로 이루어진 시퀀스 w1…wT를 훈련 세트로 사용합니다. 훈련 목표는 학습 과정에서 보지 못한 샘플에 대한 가능도를 높이는 방향으로, f(wt,⋯,wt−n+1)=ˆP(wt|wt−11)를 학습하는 것입니다. Perplexity라고도 알려진, 그리고 음의 로그 가능도(negative log likelihood)의 평균의 지수이기도 한 1/ˆP(wt|wt−11)의 기하 평균에 대해서 설명하겠습니다. 모델이 갖는 제한점은 wt−11에 대해 어떤 선택을 하든 f>0 이고,∑|V|i=1f(i,wt−1,⋯,wt−n+1)=1 뿐입니다. 확률을 계산한다는 것을 생각하면 당연한데, 결국 확률의 합이 1이고, 각 경우에 대한 확률은 양수임을 의미합니다. 다시 말하면, 모든 경우에 확률이 양수이고 그 합이 1이므로, 결국 0<f<1이라고 생각할 수 있습니다. 이 조건부 확률에 의해 단어 시퀀스의 결합 확률에 대한 모델을 얻을 수 있습니다. 여기서 함수 f(wt,⋯,wt−n+1)=ˆP(wt|wt−11)를 두 부분으로 나눌 수 있습니다.
- C는 V의 원소인 i를 실수 벡터 C(i)∈Rm으로 매핑합니다. 이는 어휘 사전 내의 각 단어와 연관된 distributed feature vector를 나타냅니다. C는 |V|×m의 가중치 행렬로 표현됩니다.
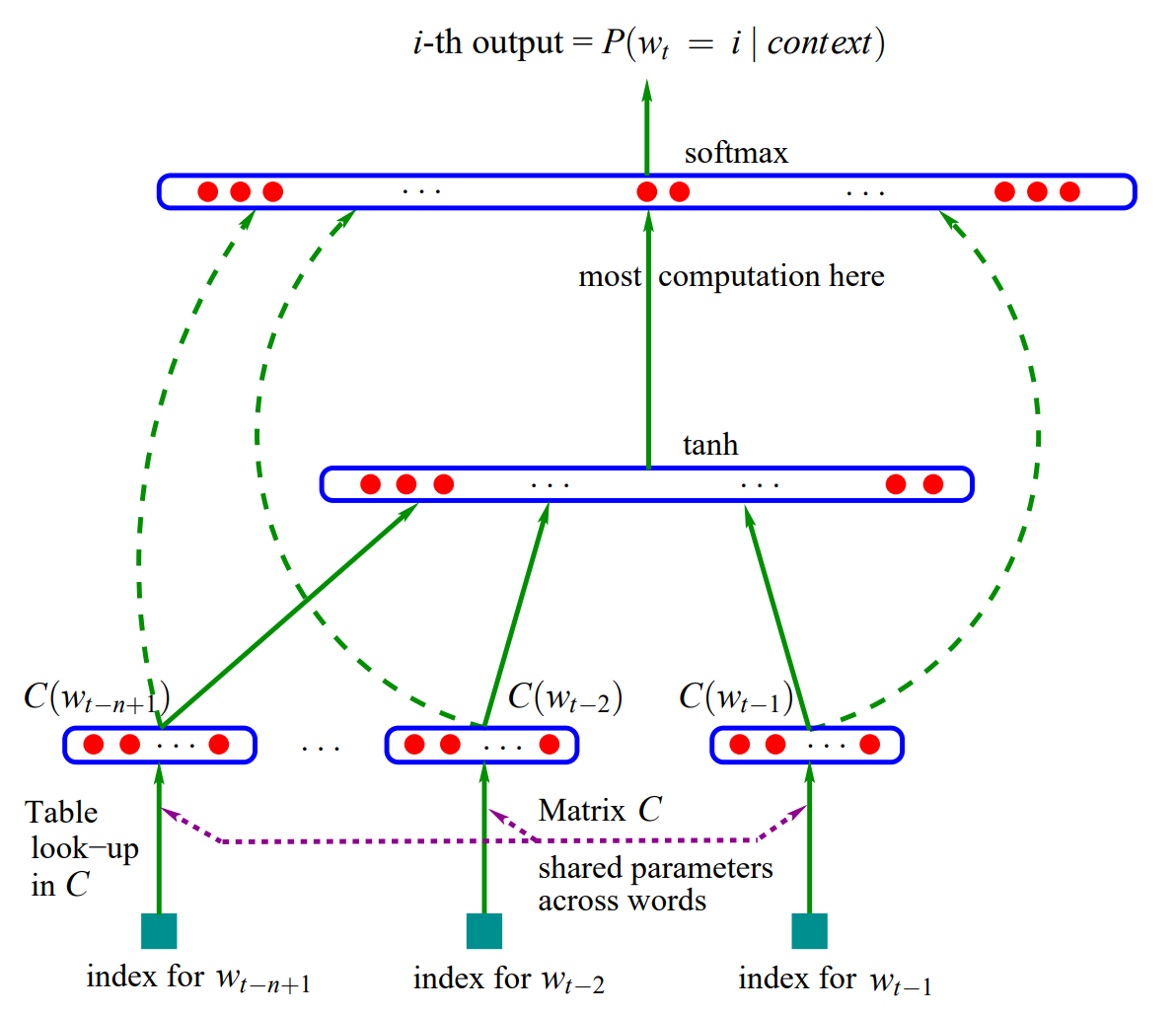
- C로 표현되는 단어에 대한 확률 함수입니다. 함수 g는 문맥 내 단어들에 대한 feactur vectors의 입력 시퀀스 C(wt−n+1),⋯,C(Wt−1)를 어휘 사전 V 안에 있는 다음 단어 wt의 조건부 확률 분포로 매핑합니다. g의 출력은 다음 그림과 같이 i번째 원소가 확률 ˆP(wt=i|wt−11)를 추정하는 벡터입니다.
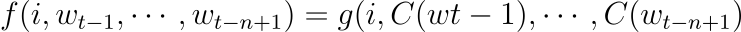
함수 f는 이러한 두 개의 매핑 C와 g로 구성되며, C는 문맥 내의 모든 단어에 대해 공유됩니다. C의 파라미터는 단순히 특성 벡터이며, C(i)는 i번째 단어의 특성 벡터를 의미합니다. g는 피드포워드, 순환 신경망 또는 다른 파라미터 ω를 갖는 함수로 구현됩니다. 전체 파라미터 집합은 \boldsymbol \theta=(C, \omega)입니다.
학습은 다음과 같이 penalized log-likelihood를 최대화하는 \theta를 찾는 것을 목표로 이루어집니다.
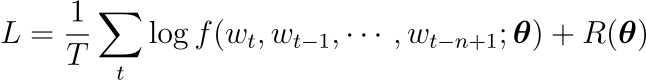
여기서 R(\boldsymbol \theta)은 규제항입니다. 실험에서 R은 편향(bias)이 아닌, 신경망과 행렬 C의 가중치에 적용된 weight decay입니다.
위 모델에서 매개변수의 수는 어휘 사전의 크기인 V에 의해 선형적으로 변합니다. 또한 차수 n에 대하여 선형적으로 변하는데, scaling factor는 sharing structure(모델 내에서 파라미터를 공유하는 부분)이 추가된다면 sub-linear하게 될 수도 있습니다.
실험에서 신경망은 word features mapping 위에 하나의 히든 레이어를 갖고, 선택적으로 word features를 출력으로 직접적으로 연결합니다. 따라서 shared word features layer인 C와 하이퍼볼릭 탄젠트 히든 레이어로 두 개의 히든 레이어를 갖습니다. 수식으로 표현하면 신경망은 다음 함수를 계산하는데, 소프트맥스와 출력 레이어를 통해 확률의 합이 1이 되도록 합니다.
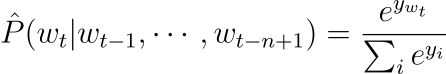
y_i는 각 단어 i에 대하여 정규화되지 않은 로그 확률이며, 파라미터 b, W, U, d, H에 대해 다음과 같이 계산됩니다.
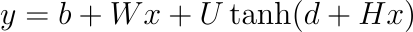
tanh는 원소별로 적용되며 W는 선택적으로 0이 되고, x는 다음 수식과 같이 입력 단어 특성을 연결한 word features layer activation vector입니다.
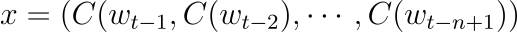
h는 hidden unit의 개수이며, m은 각 단어와 관련된 특성(features)의 개수입니다. 단어 특성과 출력 사이에 관계가 없을 경우 행렬 W는 0이 됩니다. 모델의 매개변수는 |V|개의 원소를 갖는 출력 편향 b이며, h개의 원소를 갖는 히든 레이어의 편향 d, |V| \times h 행렬인 hidden-to-output 가중치 U와 |V| \times (n-1)m 행렬인 word features to output 가중치 와 h\times(n-1)m 행렬인 hidden layer 가중치 H와 |V|\times m 행렬인 word features C입니다.
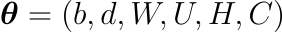
파라미터의 개수는 |V|(1+nm+h)+h(1+(n-1)m)입니다. 이 식의 dominating factor은 |V|(nm+h)입니다. 이론적으로 W와 H에는 weight deacy가 적용되고 C에는 적용되지 않는다면, W와 H는 0으로 수렴하고 C는 발산할 것입니다. 실험 중에는 SGD로 훈련할 때 이와 같은 결과를 보지 못했습니다.
신경망에서 확률적 경사 하강법(SGD)는 학습 데이터에서 t번째 단어가 나타낼 때마다 다음 작업을 반복적으로 수행합니다. 식에서 \epsilon은 학습률입니다.
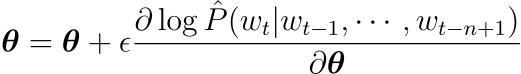
3. Parallel Implementation
파라미터의 수가 선형적으로 증가하긴 하지만, n-gram 모델의 파라미터보다는 훨씬 많습니다. 그 이유는 n-gram 모델에서는 모든 단어에 대한 확률을 계산할 필요가 없기 때문입니다. 신경망을 사용한 구현에서 주요한 computational bottleneck은 출력 레이어서의 연산에서 발생합니다. 따라서 모델을 병렬화된 컴퓨터에서 실행하면 연산 시간을 줄일 수 있습니다. 저자는 이를 위해서 shared-memory processor machine과 Linux clusters 두 가지 플랫폼에서 실험을 진행했습니다.
3.1 Data-Parallel Processing
Shared-memory processor의 경우 프로세서 사이의 낮은 communication overhead 덕분에 쉽게 병렬화가 가능합니다. 여기에는 data-parallel implementation을 적용하여 각 프로세스가 데이터의 서로 다른 부분을 작업할 수 있게 하였습니다. 각 프로세서는 각각의 데이터에 대한 그라디언트를 계산하고, stochastic gradient update를 수행한 후 shared-memory에 저장됩니다. 처음에는 연산 속도가 매우 느렸는데, 프로세스의 연산 사이클 중 대부분이 다른 프로세스의 연산을 기다리는 데 사용되었기 때문입니다.
그 대신에 asynchronous implemenation을 선택하여 각 프로세스가 shared-memory에 언제나 쓸 수 있게 하였습니다. 가끔 다른 프로세스에 의해 한 프로세스의 업데이트 내역이 덮어쓰일 때가 있었습니다. 하지만 이로 인해 발생하는 노이즈가 매우 작고 학습 속도를 눈에 띄게 느리게 하지는 않았습니다.
안타깝게도 대규모의 shared-memory parallel computer는 매우 비싸고 프로세스 속도가 CPU에 비해 느렸습니다. 따라서 fast network clusters를 통해 더 빠른 속도를 얻을 수 있었습니다.
3.2 Parameter-Parallel Processing
Parallel computer가 CPU의 네트워크라면, 프로세서 사이에서 파라미터를 충분히 빈번하게 교환할 수 없을 것이고, 로컬 네트워크에서는 너무 많은 시간이 걸릴 것입니다. 그 대신에 parallelize across the parameters를 선택하였고 특히 대부분의 연산이 이루어지는 출력 유닛의 파라미터를 선택하였습니다. 각 CPU는 출력의 일부에 대한 확률을 계산하고 그에 대응하는 출력 유닛의 파라미터를 업데이트합니다. 이 전략은 무시할 수 있는 수준의 communication overhead와 함께 parallelized stochastic gardient ascent를 가능하게 하였습니다.
4. Further Thinking
논문이 2003년에 발표된 만큼, 그리고 딥러닝과 NLP의 랜드마크 논문이라고 여겨지는 만큼 정말 중요학 심오한 내용을 많이 담고 있습니다. 앞서 읽었던 대부분의 논문보다 순수 분량도 많은 편이긴 하지만 다루는 내용도 방대하고 깊이도 매우 깊어 여태까지 정리한 내용만 해도 상당히 쉽지 않았습니다. 문장의 호흡도 길고 개념도 깊이 생각해야했던 것 같습니다. 분산 표현이나 역전파 뿐만 아니라 병렬화 등 딥러닝의 핵심적인 개념을 두루 다루는 만큼 중요하지만 더 어려웠습니다. 다시 한번 지금까지 배웠던 내용도 정리하고 다음에 읽을 내용을 이어가야겠다는 생각이 들었습니다.




댓글