
명시적인 번역 쌍을 사용하지 않고 비지도 학습을 통해 단어나 문장을 번역하는 방법론을 제안한 논문 Word Translation Without Parallel Data를 리뷰해보았습니다. 단어 임베딩이나 기계 번역 태스크 논문으로 종종 언급되는데 제안한 방법론이 새롭다는 생각이 들어서 관심갖고 읽어보게 되었습니다. 논문 자체의 길이는 길지 않지만 많은 수학적 배경지식을 요하고 추가로 정리할 내용이 꽤 많았어서 논문에서 제안한 방법론에 대한 부분과 이를 통해 수행한 실험에 대한 부분을 나눠서 정리하였습니다. 여기서는 Introduction 부터 Training and Architecture Choices, 즉 섹션 1~3만을 다룹니다. 이후 내용은 별도의 게시글에 정리할 예정입니다. 번역을 통해 오히려 이해가 어려워지거나, 원문의 표현을 사용하는 게 원래 의미를 온전히 잘 전달할 것이라고 생각하는 표현은 원문의 표기를 따랐습니다. 오개념이나 오탈자가 있다면 댓글로 지적해주세요. 설명이 부족한 부분에 대해서도 말씀해주시면 본문을 수정하겠습니다.
1. Introduction
Mikolov의 논문 Exploiting Similarities among Languages for Machine Translation은 연속 공간에서 단어 벡터의 분포가 여러 언어에서 유사한 구조를 보인다는 것을 밝혔습니다. 심지어 이런 경향은 영어와 베트남어처럼 큰 연관성이 없어 보이는 언어 쌍에서도 관찰할 수 있습니다. 언급한 논문에서는 이런 유사성을 바탕으로 소스와 타겟 임베딩 공간의 선형 매핑을 학습하는 방법을 제안하였습니다. 이 매핑을 학습하기 위해 5천 개의 단어로 구성된 병렬 어휘(parallel vocabulary)를 앵커 포인트로 사용하고 단어 번역 작업을 통해 제안한 방법을 검증하였습니다. 이후로 언어 간 단어 임베딩을 개선하기 위한 여러 연구가 진행되었지만 그들은 모두 bilingual word lexicon에 의존하였습니다.
이후 bilingual supervison, 즉 두 개의 언어에 대한 지도 학습 데이터를 사용하는 방식의 필요성을 없애기 위한 연구가 수행되었습니다. 병렬 어휘를 생성하기 위해 identical character form을 사용하는 방법이 제안되었는데 이는 유럽권 언어들처럼 공통된 알파벳을 공유하는 유사한 언어들 사이에서만 사용할 수 있는 제한적인 방법론이었습니다. 조금 더 최근의 연구는 parallel data 없이 벡터의 분포에 기반한 접근법이나 적대적 훈련을 통한 언어 간 단어 임베딩(cross-lingual word embedding)을 학습하는 방법을 탐색하였습니다. 하지만 이러한 방법은 지도 학습보다 현저하게 낮은 성능을 보였습니다. 결론적으로 이 논문이 제안되기 전까지 수행된 연구는 충분한 성능을 보이지 못하거나, 여전히 parallel data를 필요로 했습니다.
이 논문은 지도 학습된 SOTA 기법과 비슷하거나, 혹은 그 이상의 성능을 보이는 parallel data를 사용하지 않는 새로운 모델을 제안합니다. 이 모델은 두 개의 대규모 단일 언어 말뭉치만을 사용합니다. 이 기법은 두 단계에 걸친 적대적 훈련(adversarial training)을 사용하여 source space에서 target space의 linear mapping을 학습합니다. 우선 판별자(discriminator)는 매핑된 소스 임베딩과 타겟 임베딩을 각각 구분하도록 학습되고, 생성자(generator)로 생각될 수 있는 매핑은 판별자의 판별을 어렵게 하도록 학습됩니다. 이 결과로 생성된 shared embedding space에서 synthetic dictionary를 추출하고 closed-form Procrustes solution을 통해 매핑을 파인튜닝합니다. 그런데 이 기법은 비지도 학습을 사용했기 때문에 최적의 모델이 무엇인지 판단하기 어렵습니다. 이 문제를 극복하기 위하여 저자는 mapping quality와 높은 연관 관계를 가진 unsupervised selection metric을 도입하여 stopping criterion과 최적의 하이퍼파라미터를 선택하는 데 사용하였습니다.
요약하면 이 논문에서는 다음과 같은 주요 기여가 이루어졌습니다.
- 여러 언어와 세 개의 태스크에서 지도 학습된 SOTA 모델과 유사하거나 그 이상의 성능을 내는 비지도 학습 방법론을 제안하였습니다. 각 태스크는 단어 번역, 문장 번역 검색(retrieval), 언어간 단어 유사성 평가입니다.
- 도메인 간 유사도 적응(cross-domain similarity adaptation)을 도입하여 hubness problem을 완화하였습니다. 여기서 Hubness problem은 고차원 공간에서 특정 점이 수많은 점들의 최근접 이웃이 되는 경향을 갖는 문제를 말합니다. 이를 통해 모델 성능을 크게 높일 수 있었고 지도 학습과 비지도 학습을 사용한 실험 모두에서 단어 번역 벤치마크에서 기존의 SOTA 점수를 뛰어넘었습니다.
- 매핑의 품질과 밀접한 연관을 가진 unsupervised criterion을 제안하여 stopping criterion과 최적의 하이퍼 파라미터를 찾는 기준점으로 사용할 수 있게 하였습니다.
- 높은 품질을 갖는 12개의 언어 쌍과 이들에 대응하는 supervised, unsupervised word embedding을 배포하였습니다.
- 에스페란토어와 같이 데이터가 적은 언어에 대한 검증을 통해 제안된 기법의 효용을 입증하였습니다.
2. Model
먼저 이 논문에서 수행한 모든 실험은 각각의 단일 언어 데이터를 사용하여 독립적으로 학습된 두 개의 단어 임베딩 집합을 사용한다고 가정합니다. 이 연구는 비지도 학습을 통해 이 두 집합 사이의 매핑을 학습하여 shared space에서 번역쌍이 서로 가까워지게 하는 것을 목표로 합니다. Mikolov는 monolingual embedding space이 갖는 유사성을 이용해 이런 매핑을 학습할 수 있음을 밝혔습니다. 이를 위해서 n=5000 쌍의 단어 쌍으로 된 사전 xi,yii∈1,n을 사용하여 소스와 타겟 공간의 선형 매핑 W를 학습해야 합니다.

수식에서 d는 임베딩의 차원을 의미하며, Md(R)은 실수로 이루어진 d×d 행렬 공간입니다. X와 Y는 d×n 크기의 병렬 어휘에 포함된 단어 임베딩에 대한 두 개의 aligned matrices입니다. 원본 단어 s의 번역 t는 t=argmaxtcos(Wxs,yt)으로 정의됩니다.
Mikolov는 단어 번역 태스크에서 단순한 선형 매핑만을 사용하여 더 나은 결과를 얻었지만, 신경망과 같이 더욱 고도화된 전략을 사용한 방법으로는 별도의 성능 향상이 없었습니다. Xing의 연구에서 W에 orthogonality constraint를 부여하면 이를 개선할 수 있음을 밝혔습니다.
여기서 orthogonality constraint는 어떤 행렬이 orthogonal 하도록 제약을 거는 것입니다. Orthogonal을 먼저 벡터 차원에서 정의하면 자기 자신 외에 다른 벡터와의 내적은 0이 되는 성질을 의미합니다. 여기서 나아가 자기 자신과의 내적이 1이 되면 이 벡터는 orthonormal하다고 합니다. Orthogonal matrix는 행렬의 행과 열이 모두 orthonormal한 정사각행렬을 말합니다. 즉 WTW=WWT=I 을 만족하는 경우를 의미합니다. Orthogonal transformation은 벡터 간의 유클리드 거리와 각도를 보존하기 때문에 단어 임베딩과 같이 상대적인 거리가 의미론적 유사성을 반영하는 경우 매우 중요합니다. 또한 그 자체로 최적화 등의 연산의 단순함을 보장하고 규제로써의 역할을 하기 때문에 유용합니다.
돌아와서 위 내용을 바탕으로 앞에서 본 수식은 Procrustes problem으로 귀결되고, 이는 YXT의 특잇값 분해(SVD)에서 얻은 closed form solution를 제공합니다.

논문에서는 언어 간 지도학습 없이 매핑 W를 학습하는 방법을 보입니다. 이 과정은 다음 그림을 통해 이해할 수 있는데, 먼저 adversarial criterion을 사용하여 W의 초기 형태를 학습합니다. 그 다음에 가장 잘 매치되는 단어를 Procrustes의 앵커 포인트로 사용합니다. 마지막으로 벡터 공간의 metric을 바꿔가며 낮은 빈도로 나타나는 단어에 대한 성능을 향상합니다. 이 과정에서 밀집된 공간에 위치한 점들을 분산시킬 수 있습니다. 이제 각 과정에 대하여 자세히 알아보겠습니다.

그림에 대해서 논문의 설명을 사용하여 다시 한 번 설명해보겠습니다. (A) 두 개의 단어 임베딩에 대한 최초의 분포가 존재합니다. 빨간 색은 영어 단어에 대한 분포이며 X로 표시되며, 파란 색은 이탈리아 단어의 분포이며 Y로 표시합니다. 이 단어를 번역하는 게 목표이며, 이는 두 분포를 align하는 것을 의미합니다. 점의 크기는 각 단어의 등장 빈도와 관련됩니다.
(B) 적대적 학습을 통해 두 분포를 대략적으로 align하는 회전 행렬(rotation matrix) W를 학습합니다. 초록색 별은 임의로 선택된 단어이며 판별자에 입력되어 이 단어가 같은 임베딩 공간에서 추출한 것인지를 판단하게 합니다.
(C) 매핑 W는 Procrustes를 통해 조정됩니다. 이 방법은 이전 단계에서 align된 자주 사용되는 단어를 anchor point로 사용합니다. 이를 통해 앵커 포인트간의 spring system에 대응하는 energy function을 최소화하게 됩니다. 즉, 자주 등장하는 단어인 앵커 포인트에 대하여, 드물게 나타나는 단어의 최적의 위치를 찾기 위한 과정을 의미합니다. 이 과정을 통해 얻은 refined mapping은 사전의 모든 단어를 매핑하는 데 사용됩니다.
(D) 마지막으로 매핑 W와 distance metric을 사용하여 번역을 수행합니다. 이 과정에서 사용되는 CSLS는 점의 밀도가 높은 공간을 확장하여 hub가 다른 단어 벡터들과 덜 가까이 위치하도록 합니다. 예를 들어 (A)와 (D)에서 cat 주변의 점들을 보면 점들이 조금 더 멀리 퍼진 것을 알 수 있습니다.
참고로 위에서 언급한 closed-form solution은 반복적인 과정이나 근사 등을 요구하지 않고 단순하게 해를 구할 수 있는 경우를 의미합니다. 예를 들면, 각 항의 계수에 숫자만을 대입하여 해를 구할 수 있는 근의 공식을 생각할 수 있습니다. 반면 non closed-form은 ∫e−x2dx와 같이 수식의 근사를 위한 특별한 기법이 요구되는 경우를 의미합니다.
2.1 Domain-Adversarial Setting
여기서는 cross-lingual supervision 없이 W를 학습하기 위한 domain-adversarial approach에 대해서 집중적으로 알아보겠습니다. 먼저 X=x1,…,xn과 Y=y1,…,ym을 각각 source와 target 언어에 대한 n과 m개의 단어 임베딩 집합이라고 정의합니다. 모델은 WX=Wx1,…,Wxn과 Y에서 임의로 추출한 원소를 구별하도록 훈련됩니다. 이 모델은 판별자라고 부르겠습니다. W는 판별자가 정확한 예측을 하기 어렵게 하도록 훈련됩니다. 결과적으로이는 판별자는 임베딩의 유래가 어디인지를 구분하는 능력을 최대화하고, W는 WX와 Y를 최대한 비슷하게 만들어 판별자가 이를 구분하기 어렵게 만드는, 두 명의 플레이어가 수행하는 게임이라고 생각할 수 있습니다. 이 방식은 입력 도메인에 따라 변하지 않는 잠재 표현(latent representation)을 학습하는 기법을 제안한 Ganin의 연구와 관련되어 있으며, 이 논문에서는 그 도메인이 언어에 해당하는 것 뿐입니다.
Discriminator objective
판별자 파라미터를 θD라고 정의합니다. 벡터 z가 판별자에 의해 타겟 임베딩이 아닌 소스 임베딩의 매핑이 될 확률 PθD=(source=1|z)에 대해 생각하겠습니다. 그러면 판별자의 손실 함수는 다음과 같이 나타낼 수 있습니다.
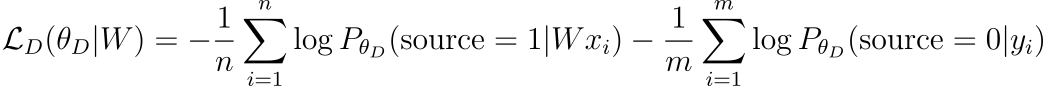
GAN 개념에 익숙하다면 이 손실 함수의 의미를 파악하기 쉽겠지만, 그렇지 않다는 가정 하에 판별자의 손실 함수에 대하여 자세히 알아보겠습니다. 같은 방법으로 매핑의 손실 함수도 해석할 수 있습니다. 먼저 좌변은 매핑 W가 주어졌을 때 판별자 파라미터 θD에 의해 결정되는 판별자의 손실을 의미합니다. 우변은 이를 정의하는 방식인데, 비슷한 모양의 항이 연결되어 있습니다.
첫 번째 항에서 로그 함수 안쪽을 먼저 보겠습니다. 원본 언어의 단어의 벡터, 즉 source embedding의 한 벡터와 매핑 W에 대한 곱 Wxi가 주어졌을 때 이 값이 source embedding에서 유래했을 확률을 PθD(source=1|Wxi)을 계산하는 것입니다. 당연히 xi는 source embedding의 벡터이기 때문에 이 확률이 커져 1에 가까울수록 좋습니다. 반대로 손실은 작을수록 좋기 때문에 로그를 취한 뒤 음수로 만들어 확률이 1에 가까워질수록 손실에 0에 가까운 값이 더해지게 합니다.
마찬가지로 두 번째 항은 목표 언어의 단어 벡터 yi가 source embedding에서 유래하지 않았을 확률PθD(source=0|yi)를 계산합니다. Target embedding에서 유래했기 때문에 source=0을 만족하는 확률은 커져야합니다. 앞에서 설명한 것과 같은 원리로 손실은 작아져야 하므로 음의 로그를 취하여 확률이 커지면 손실이 작아지도록 합니다.
Mapping objective
반면에 비지도 학습 환경에서 W는 판별자가 임베딩의 유래(embedding origin)에 대한 정확한 예측을 하지 못하도록 훈련됩니다.
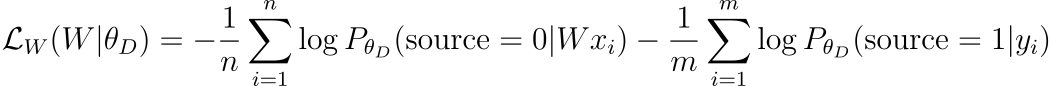
Learning Algorithm
논문의 모델을 훈련하기 위해서 Goodfellow가 제안한 deep adversarial network의 표준 훈련 과정을 따릅니다. 모든 입력 샘플에 대하여 판별자와 매핑 행렬 W는 연속적으로 stochastic gradient update를 통해 각각의 손실 함수인 LD와 LW를 최소화하도록 훈련됩니다.
2.2 Refinement Procedure
적대적 훈련을 통해 얻은 행렬 W는 괜찮은 성능을 보이지만, 지도 학습을 통해 훈련된 모델에 미치지는 못합니다. 사실 이 방식은 빈도에 관계없이 모든 단어를 align하려는 목표를 갖습니다. 하지만 희귀 단어의 임베딩은 자주 업데이트되지 않을 뿐만 아니라 각 말뭉치에서 매우 다른 문맥에서 등장할 가능성이 높습니다. 이런 점은 희귀 단어의 align을 어렵게 만듭니다. 매핑이 선형적이라는 가정 하에 자주 등장하는 단어를 앵커 포인트로 사용하여 global mapping을 추론하는 게 더 나을 것입니다. 게다가 이런 단어들에 대한 정확도는 적대적 훈련 결과만 봐도 상당히 높습니다.
매핑을 개선하기 위해서 적대적 훈련을 통해 학습된 W를 사용하여 synthetic parallel vocabulary를 구축하였습니다. 특히 가장 많이 사용된 단어만을 고려하여 mutual nearest neighbors만을 유지하여 어휘의 품질을 높였습니다. 이후 생성된 사전에 앞에서 언급한 Procrustes 알고리즘을 적용하였습니다. 이 알고리즘을 통해 생성된 improved solution을 고려하면 더욱 정교한 사전을 생성할 수 있을 것입니다. 또한 이 과정을 반복적으로 수행하면 점점 더 사전의 품질은 향상됩니다. 하지만 synthetic dictionary가 이미 좋은 성능을 보인 적대적 훈련의 결과를 사용한다는 점에서, 실제로는 1 iteration 이상 이 과정을 반복하면 성능이 큰 폭으로 향상되지는 않았습니다.
2.3 Cross-Domain Similarity Local Scaling (CSLS)
이제 두 언어 사이의 신뢰할 수 있는 matching pair를 생성하는 방법을 생각해보겠습니다. 목표는 source word의 최근접 이웃이 target word에서도 최근접 이웃이 되도록 comparison metric을 개선하는 것입니다.
최근접 이웃은 본질적으로 비대칭성을 갖습니다. 즉 y가 x의 K-NN임이 x가 y의 K-NN임을 보장하지는 않습니다. 고차원 공간에서 이는 최근접 이웃 규칙에 따라 단어 쌍을 매칭하는 데 매우 불리하게 작용합니다. Hub라고 불리는 일부 벡터는 다른 많은 점의 최근접 이웃이 될 확률이 높지만, 다른 벡터(anti-hub)는 그 어떤 점의 최근접 이웃이 되지 않을 수도 있습니다.
이런 문제를 해결하기 위한 여러 방법이 제안되었지만 기존의 연구는 대부분 single feature distribution만을 가정합니다. 하지만 논문의 연구에서는 각각 하나의 언어에 대응하는 두 개의 도메인을 고려해야 합니다. 이와 관련해서 Dinu는 reverse rank 기반한 paring rule을 제안하였고, Smith는 inverted soft-max(ISF)를 제안하였습니다. 이 두 가지에 대해서는 실험 섹션에서 자세히 다룹니다. 그런데 이러한 방법은 원본 언어와 목표 언어의 단어에 대한 similarity update가 다르기 때문에 완전히 만족스럽지는 않습니다. 또한 ISF는 파라미터의 교차 검증을 필요로 하기 때문에, 이 실험에서와 같이 비지도 학습 환경에서는 추정치에 노이즈가 많을 것이라는 문제가 있습니다.
이 실험에서는 사전의 각 단어가 다른 언어에서 K개의 최근접 이웃과 연결된 bi-partite neighborhood graph를 사용합니다. NT(Wxs)를 이분 그래프(bi-partite graph)에서 mapped source word embedding Wxs과 연관된 이웃으로 정의합니다. NT(Wxs)의 모든 K개의 원소는 목표 언어의 단어입니다. 마찬가지로 NS(yt)를 목표 언어의 단어 t와 연관된 이웃으로 정의합니다. 그리고 소스 임베딩 xs과 그에 대응하는 target neighborhood의 평균 유사도를 다음과 같이 정의합니다.
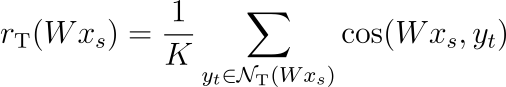
수식에서 cos은 코사인 유사도를 의미합니다. 마찬가지로 rS(yt)를 목표 단어 yt와 그의 이웃과의 평균 유사도로 정의합니다. 각각의 값은 모든 source 및 target 단어 벡터에 대해서 계산됩니다. 그리고 이를 바탕으로 mapped source words와 target words의 유사도 지표 CSLS를 다음과 같이 정의합니다.
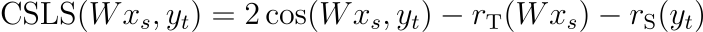
직관적으로 이 과정을 통해 고립되어 있는 단어 벡터와의 연관성이 증가할 것임을 알 수 있습니다. 반대로 밀집된 공간에 있던 벡터의 유사도는 감소할 것입니다. 저자는 실험을 통해 CSLS가 파라미터 튜닝 없이 단어 번역 검색의 성능을 상당히 향상한다는 것을 입증하였습니다.
3. Training and Architectural Choices
3.1 Architecture
이 연구에서는 fastText를 사용하여 비지도 학습된 단어 벡터를 사용하였습니다. 이는 Wikipedia 말뭉치를 통해 학습된 300차원의 단일 언어 임베딩입니다. 따라서 매핑 W의 크기도 300×300 입니다. 단어는 소문자로 정규화되었고 5번 미만으로 등장하는 단어는 학습에서 제외하였습니다. 후처리 단계에서는 20만 개의 자주 등장하는 단어만을 선택하여 실험에 사용하였습니다.
판별자는 2048차원을 갖는 두 개의 히든 레이어와 Leaky-ReLU 활성화 함수로 이루어진 다층 퍼셉트론을 사용하였습니다. 판별자의 입력으로 0.1의 dropout을 적용하였고 Goodfellow의 연구에 따라 판별자 예측에 smoothing coefficient s=0.2를 사용하였습니다.
3.2 Discriminator Inputs
일반적으로 희귀 단어에 대한 임베딩의 품질은 자주 등장하는 단어에 비해서 좋지 못합니다. 그리고 저자는 판별자에 희귀 단어를 입력하는 것이 작지만 무시할 수 없는 부정적 영향을 미치는 것을 관찰하였습니다. 따라서 판별자에는 5만개의 가장 자주 등장하는 단어만을 입력으로 사용하였습니다. 각 training step에서 판별자에 입력되는 단어 임베딩은 균일 분포에서 임의로 선택하였습니다. 참고로 단어 빈도에 따라 샘플링하는 방법은 눈에 띄는 영향을 미치지는 않았습니다.
3.3 Orthogonality
Smith는 선형 연산에 orthogonal constraint를 부여하면 더 좋은 성능을 보임을 밝혔습니다. 직교 행렬(orthogonal matrix)를 사용하는 것은 몇가지 이점이 있는데, 앞서 언급했듯 임베딩의 monolingual quality를 보존합니다. 실제로 직교 행렬은 벡터의 내적, ℓ2 distance를 보존하기 때문에 이에 따라 유클리드 공간에서의 isometry를 보존하게 됩니다. 게다가 이 실험에서는 orthogonality가 학습 과정에 안정성을 더해주었습니다. 이 연구에서는 행렬 W가 학습 과정에서 직교 행렬과 가까운 형태를 유지하도록 하는 간단한 업데이트를 제안하였습니다. 수식에서 β=0.01을 사용하였습니다.
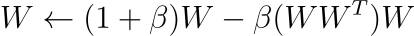
3.4 Dictionary Generation
Refinement step은 각 iteration마다 새로운 사전을 생성할 것을 필요로 합니다. Procrustes solution이 잘 동작하기 위해서는 올바른 단어 쌍이 필요합니다. 따라서 저자는 CSLS를 사용하여 사전에서 정확도가 높은 번역 쌍을 선택하였습니다. 또한 사전의 품질을 더욱 높이고 W가 올바른 번역 쌍을 학습하도록, mutual nearest neighbor만을 고려하였습니다. 이 방법은 사전의 크기를 매우 작게 만들지만, 그만큼 정확도가 높아져서 전반적인 성능이 향상되었습니다.
3.5 Validation Criterion for Unsupervised Model Selection
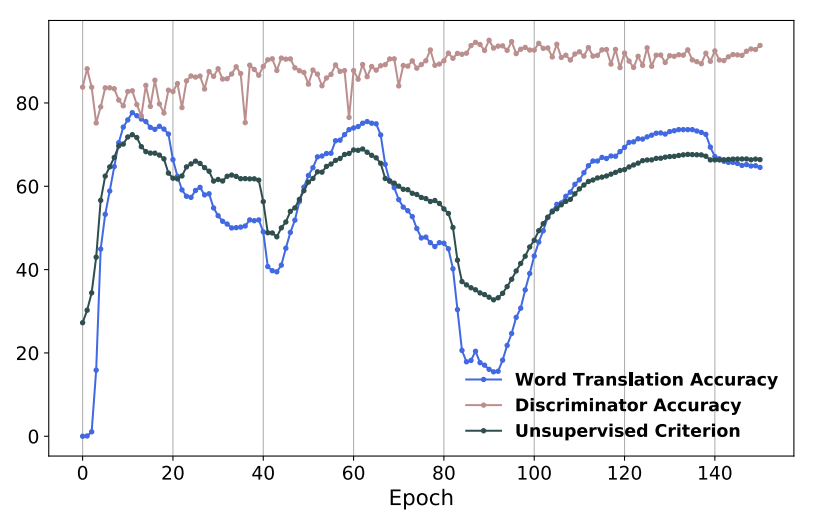
비지도 학습에서 검증 세트를 사용할 수 없는 상황에서 최적의 모델을 찾는 것은 어렵지만 매우 중요한 작업입니다. 이 문제를 해결하기 위해서 source와 target 임베딩 공간의 거리를 정량화하는 unsupervised criterion을 사용하였습니다. 1만 개의 자주 사용되는 source word를 사용하여 CSLS를 통해 각각에 대응하는 번역을 생성하였습니다. 그리고 이 잠재 번역 단어와의 평균 코사인 유사도를 계산하여 검증 지표로 사용하였습니다. 저자는 이 방법이 Wasserstein distance와 같은 optimal transport distance 보다 더 좋은 지표임을 실험을 통해 발견하였습니다. 다음 그림은 검증 점수와 unsupervised criterion의 상관관계를 보여줍니다. 이 지표는 학습 과정에서 stopping criterion과 하이퍼 파라미터 선택을 위해서 사용되었습니다.
모든 내용을 정리한 게 아니라 회고를 작성하기에는 이르지만, SVD를 포함하여 선형대수학의 고급 개념을 많이 다루어서 특히 이해하는 데 오래 걸렸던 논문이었습니다. 그마저도 배경지식 없이 그때 그때 관련 개념을 찾아서 공부하다보니 수식 전개나 근사하는 과정을 완전히 이해하지 못한 부분이 있는 것 같습니다. 논문의 후반부를 마저 정리하고 관련 개념을 다시 한 번 학습해야겠다는 생각이 들었습니다. 특히 NLP 논문을 읽을수록 선형대수학이나 최적화와 관련된 공부가 필요하다는 걸 계속해서 깨닫게 되는 것 같습니다.
'Paper Review' 카테고리의 다른 글
| [논문리뷰] Training language models to follow instructions with human feedback (0) | 2023.11.10 |
|---|---|
| [논문리뷰] Word Translation Without Parallel Data (2) (0) | 2023.11.05 |
| [논문리뷰] Enriching Word Vectors with Subword Information (1) | 2023.10.29 |
| [논문리뷰] GloVe: Global Vectors for Word Representation (1) | 2023.10.27 |
| [논문리뷰] Attention Is All You Need (1) | 2023.10.24 |




댓글