다양한 성능 평가 지표
머신러닝 모델의 대표적인 예측 성능 평가 지표는 정확도, 재현율, 정밀도와 이를 기반으로 한 F1 점수가 있습니다. 이 뿐만 아니라 태스크와 도메인에 따라 수많은 평가지표가 존재하고, 하나의 태스크에 대해 다양한 평가 지표를 적용하기도 합니다. 해결하려는 문제에 따라서 모델을 평가하는 방법도 달라지기 때문입니다. 그렇다면 앞서 언급한 네 가지 평가 지표는 각각 어떤 역할을 할 지 알아보겠습니다.
머신러닝 모델의 예측 성능을 평가하는 지표는 정말 다양합니다. 실제로 위키피디아의 머신러닝 평가 지표(Machine learning evaluation metrics) 표를 보면 대충 봐도 수십 개의 지표가 나열되어 있습니다. 이 지표들도 전체에 비하면 극히 일부일 뿐입니다. 이처럼 다양한 평가 지표가 존재하는 이유는, 해결하려고 하는 문제나 다루는 데이터에 따라서 다른 평가 기준이 필요하기 때문입니다. 바꿔 말하면, 태스크나 도메인에 따라 수많은 평가지표가 존재합니다. 게다가 하나의 문제에 여러 가지 평가 지표를 적용하기도 합니다.

예측의 정확도를 측정하기
점수를 매길 때 가장 간단하게 사용할 수 있는 방법은 단순히 전체 문제 중에 정답의 개수를 확인하는 것입니다. 이를 정확도(accuracy)라고 하는데, 머신러닝에서는 문제에 대해 모델이 내놓은 정답을 예측(predictions)이라고 표현하므로, 이를 수식으로 나타내면 다음과 같을 것입니다.

정확도는 대부분의 상황에서 일반적으로 사용할 수 있는 평가 지표이며, 직관적이며 계산도 쉬워서 유용합니다. 하지만 빠르고 간단한 만큼 단점도 분명히 존재합니다. 특히 예측해야 하는 클래스에 불균형이 존재할 경우, 높은 정확도는 거의 의미가 없어집니다.
콜롬비아의 부에나벤투라(Buenaventura)라는 곳은 일년 중 258일 비가 온다고 합니다. 이곳의 날씨를 예측하는 프로그램을 만든다고 생각해보겠습니다. 그러면 정확도가 70%인 모델을 만드는 데 코드 단 두 줄이면 충분합니다.
def is_rainy(data):
return True
365일 중 258일 비가 오기 때문에, 무조건 비가 온다고 예측하여도 평균적으로 70% 정도는 정답을 맞출 것입니다. 물론 이는 데이터의 편향을 학습한 편법일 뿐이지만, 이처럼 불균형이 존재할 경우 정확도가 갖는 문제로 인해 가능한 일입니다. 이처럼 정확도는 클래스 불균형이 존재할 경우 모델 성능 측정 지표로써의 신뢰도가 상당히 떨어집니다.
이 뿐만 아니라 정확도는 틀린 문제는 왜 틀렸는지를 알 수가 없습니다. 위와 같이 이진 분류 문제에서 오답 유형(type of error)은 두 가지가 있습니다. 비가 오는데 오지 않는다고 예측한 경우와 비가 오지 않는데 온다고 예측한 경우입니다. 때로는 이 둘을 구분하여 모델의 성능을 개선할 방안을 모색할 필요가 있습니다. 그런데 정확도만으로는 이를 구분하기 어렵습니다. 이 개념을 조금 확장하여, 더 많은 클래스가 존재할 때, 각 클래스에 대한 성능을 구체적으로 알기도 어렵습니다.
오답의 원인 알아보기
이런 문제를 해결하기 위해서 등장한 개념이 정밀도(precision)와 재현율(recall) 입니다. 정밀도와 재현율은 정보 검색(information retrieval)에서 유래하였다는 말이 있는데, 각각의 개념은 조금 뒤에 알아보겠습니다.
이진 분류 문제에서는 보통 데이터가 어떤 성질을 가지는지, 갖지 않는지를 판단합니다. 이 때, 해당 성질을 가질 경우 양성 샘플(positive sample)이라고 하고, 그렇지 않을 경우 음성 샘플(negative sample)이라고 합니다. 각 지표를 정의하기 위해서는 먼저 TP(True Positive), FP(False Positive), FN(False Negative), TN(True Negative) 개념을 알아야 합니다. TP와 TN은 문자 그대로 양성 샘플과 음성 샘플을 각각 올바르게 구분한 경우입니다. FP는 실제로는 음성인데, 양성으로 잘못 분류한 경우이며, 1종 오류(type 1 error)라고 부르기도 합니다. 마찬가지로 FP는 실제로는 양성인데 음성으로 잘못 분류한 경우이며 2종 오류(type 2 error)라고 부르기도 합니다.
이 네 가지 경우를 다음과 같이 혼동 행렬(confusion matrix)로 표현하기도 합니다.

이 혼동 행렬을 바탕으로 앞서 언급한 정확도를 다시 정의하면 다음과 같이 표현할 수 있습니다.

이제 혼동 행렬을 통해서 오답이 어떤 유형에 속하는지를 파악할 수 있습니다. 그러면 정밀도와 재현율은 무엇일까요? 먼저 각각을 수식으로 정의하면 다음과 같습니다.

각 개념을 설명하면, 정밀도는 양성 예측의 정확도로, 양성이라고 예측한 데이터 중 실제로는 몇 개가 양성인지를 의미합니다. 반면 재현율은 모든 양성 샘플 중에 몇 개를 양성이라고 예측했는지를 의미합니다. 정밀도와 재현율을 처음 접하면 항상 헷갈리는데, 예시와 함께 다시 한 번 알아보겠습니다. 예를 들어서 코로나19를 진단하는 키트를 생각해보겠습니다. 이 때 정밀도는 코로나에 감염되었다고 진단한 환자 중 실제 감염자의 비율입니다. 반대로 재현율은 전체 감염자 중 몇 명을 가려냈는지를 의미합니다. 정확도와 재현율은 상황에 따라 중요도가 다릅니다.
코로나19 예시의 경우 심각도를 어떻게 보냐에 따라 의견이 달라질 수 있기 때문에 다른 예시를 통해 설명해보겠습니다. 흔히 스팸 필터링과 도난 방지 카메라를 예시로 들곤 합니다. 먼저 스팸 메일을 필터링하는 경우를 생각해보겠습니다. 여기서 중요한 것은 정밀도일까요, 아니면 재현율일까요? 정밀도가 높다는 것은 스팸이라고 분류한 메일 중 실제 스팸 메일인 경우가 많다는 것입니다. 반대로 재현율이 높다는 것은 전체 스팸 메일 중 얼마 만큼이나 걸러내었는지를 의미합니다. 정밀도가 낮으면 스팸이 아닌데 스팸이라고 하는 경우가 많을 것이며, 재현율이 낮으면 많은 스팸 메일을 걸러내지 못할 것입니다. 여기서는 일반적으로 높은 정밀도가 선호됩니다. 낮은 정밀도를 가진 스팸 메일 필터가 중요한 업무 메일을 스팸으로 분류하는 상황이, 스팸 메일을 걸러내지 못하고 노출하는 경우보다 치명적일 것입니다.
다음으로 도난 방지 카메라의 경우를 생각해보겠습니다. 높은 정밀도는 도둑이 들었다는 신호를 울렸을 때, 실제로 도둑이 들었을 경우를 판단합니다. 반대로 재현율은 도둑이 들었을 때 얼마나 잘 잡아내는지를 의미합니다. 이 상황에서는 앞에서와는 다르게 재현율이 매우 중요합니다. 낮은 정밀도로 인하여 실제로는 도둑이 들지 않았는데도 잘못된 알림이 울리는 경우보다, 낮은 재현율 때문에 도둑이 들었는데도 알아채지 못하는 경우가 훨씬 치명적입니다. 이와 같이 상황에 따라 정밀도가 중요할 수도, 재현율이 중요할 수도 있습니다.
정밀도 재현율 트레이드오프
그냥 정밀도와 재현율을 모두 높이는 방향으로 모델을 설계하면 되는데, 왜 그렇지 않을까요? 안타깝게도 정밀도와 재현율을 모두 얻을 수는 없습니다. 정밀도가 높아지면 재현율이 낮아지고, 반대도 마찬가지입니다. 이 현상을 정밀도/재현율 트레이드오프(precision-recall tradeoff)라고 합니다.
분류기는 결정 함수(decision function)를 사용하여 각 샘플에 대해 점수를 계산합니다. 점수가 임곗값보다 크면 양성으로, 작으면 음성으로 판단합니다. 다음과 같이 숫자가 5인지 아닌지를 분류하는 이진 분류기가, 각 샘플을 점수에 따라 나열한 상황에서 결정 임곗값(threshold)에 따른 정밀도와 재현율을 살펴보겠습니다. 먼저 결정 임곗값이 가운데 화살표일 때 정밀도와 재현율은 각각 80%, 67%입니다. 여기서 정밀도를 높이기 위해 임곗값을 오른쪽으로 이동하면 재현율이 낮아집니다. 반대로 재현율을 높이기 위해 임곗값을 왼쪽으로 이동하면 정밀도가 낮아집니다. 이처럼 정밀도와 재현율을 모두 최대로 할 수는 없습니다.

정밀도와 재현율을 모두 고려한 F1 점수
이처럼 정밀도와 재현율 사이에는 트레이드 오프가 존재하지만, 둘 모두를 고려해야 하는 상황도 분명히 존재합니다. 가장 간단한 방법은 두 점수를 평균한 점수를 사용하는 것인데, 흔히 정밀도와 재현율의 산술 평균보다는 조화 평균(harmonic mean)을 사용합니다.
정밀도와 재현율의 조화 평균을 F1 점수(F1 score)라고 하며, 다음과 같이 계산합니다.
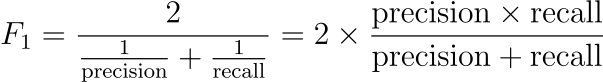
앞에서 언급했듯이 결정 임곗값을 어떻게 정하느냐에 따라서 정밀도와 재현율은 달라질 수 있습니다. 사이킷런(scikit-learn) 라이브러리에서 precision_recall_curve 함수를 사용하면, 다음과 같이 임곗값(threshold)에 따른 정밀도와 재현율을 확인할 수 있습니다.

참고로 F1 점수는 다음 식에서 $\beta$의 값이 1일 때를 의미합니다. 여기서 $\beta$가 1보다 크면 재현율이 강조되고, 1보다 작으면 정밀도가 강조됩니다. 따라서 중요하게 생각하는 지표에 따라 F 점수를 조정할 수 있습니다.
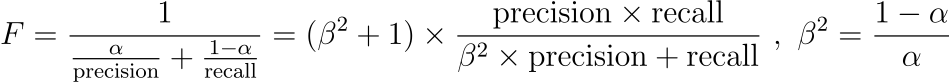
이 외에도 ROC 커브, Macro와 Micro F1 점수 등 앞서 언급한 지표들과 관련한 개념들이 매우 많습니다. 하나의 게시글에서 모든 내용을 다루기에는 내용이 과도하게 많아질 것 같아서, 이 부분에 대해서는 추후 이어서 정리하겠습니다. 여기서 언급한 정확도, 정밀도, 재현율, F1 점수는 모두 이진 분류 문제를 푸는 상황에 대하여 설명하였습니다. 그런데 하나의 지표를 여러 가지 문제에 적용할 수도 있고, 반대로 같은 문제에도 다양한 평가 지표를 적용할 수도 있습니다. 결국 자신이 풀고자 하는 문제에 적합한 지표를 정하고, 모델이 더 나은 방향으로 학습할 수 있도록 하는 것이 중요합니다.
'ML, DL Basic' 카테고리의 다른 글
| 딥러닝 논문을 읽는 방법 (0) | 2023.11.03 |
|---|---|
| Attention과 Query, Key, Value (1) | 2023.10.26 |
| Hierarchical Softmax 자세히 알아보기 (0) | 2023.10.20 |
| 딥러닝의 역사 알아보기 (2) | 2023.10.18 |
| BLEU 지표의 등장과 한계 (0) | 2023.09.11 |




댓글