
입력의 각 특성이 모델의 예측에 영향을 미치는 정도를 의미하는 feature importance를 계산하는 여러 가지 방법에 대해서 깊게 탐구하고, 이를 바탕으로 새로운 방식인 SHAP를 제안하는 논문인 A Unified Approach to Interpreting Model Predictions를 리뷰해보았습니다. 번역을 통해 오히려 이해가 어려워지거나, 원문의 표현을 사용하는 게 원래 의미를 온전히 잘 전달할 것이라고 생각하는 표현은 원문의 표기를 따랐습니다. 오개념이나 오탈자가 있다면 댓글로 지적해주세요. 설명이 부족한 부분에 대해서도 말씀해주시면 본문을 수정하겠습니다.
1. Overview
예측 모델의 출력을 올바르게 해석하는 것은 모델의 예측 정확도를 높이는 것 만큼이나 매우 중요합니다. 이는 사용자의 신뢰와 직결될 뿐만 아니라 모델이 어떻게 개선될 수 있을지에 대한 인사이트를 제공하고 모델링 과정에 대한 이해를 돕습니다. 일부 사례에서는 선형 모델과 같이 단순한 모델이 복잡한 모델보다 정확성이 떨어질 수 있음에도 불구하고, 해석이 쉽다는 이유로 선호됩니다. 하지만 대규모 데이터를 이전보다 더 많이 사용할 수 있게 됨에 따라 복잡한 모델의 이점이 증가했습니다. 이에 따라 모델 출력의 정확성과 해석 가능성 사이의 균형(trade-off)을 찾을 필요가 있었습니다. 이 문제를 해결하기 위한 다양한 방법이 제안되었습니다. 하지만 제안된 방법들 사이에 어떤 관계가 있는지, 그리고 한 방법이 다른 방법에 비해 언제 선호되어야 하는지에 대한 이해가 여전히 부족했습니다. 저자는 이 논문을 통해 모델 예측을 해석하기 위한 새로운 통합된 접근법을 제안합니다. 이 접근법은 세 가지 놀라운 결과를 보여주며, 위에서 언급한 문제에 명확성을 가져다줍니다.
먼저 저자는 모델의 예측에 대한 설명을 하나의 모델로 보는 새로운 시각을 도입하고, 그러한 모델을 explanation model이라고 부릅니다. 이를 통해 당시에 제안된 여섯 가지 접근법을 통합하는 additive feature attribution methods를 정의합니다.
그 다음으로 저자는 게임 이론의 결과가 유일해를 가짐을 보장한다는 것이 additive feature attribution methods의 모든 클래스에 적용 가능함을 입증하며, 특성 중요도를 측정하는 통합된 지표로써 SHAP values를 제안합니다.
새로운 SHAP 측정 방식을 제안하고 이 방법이 사람의 직관과 잘 맞고 기존 접근법에 비해 더욱 효과적으로 모델의 출력 클래스를 구분한다는 것을 보입니다.
2. Additive Feature Attribution Methods
단순한 모델에 대해서 최고의 설명은 모델 그 자체이다.
모델은 자기 자신을 완벽하게 설명하고 이해하기도 쉽습니다. 하지만 앙상블과 심층 신경망과 같이 복잡한 모델은 이해하기 쉽지 않기 때문에 원본 모델을 그대로 사용하여 설명하기는 어렵습니다. 대신 더 단순한 explanation model을 사용합니다. 저자는 explanation model이 원본 모델을 해석 가능하도록 근사한 것(interpretable approximation)이라고 정의합니다. 저자는 기존 연구에서 제안된 여섯 개의 설명 방식(explanation methods)는 모두 같은 explanation model을 사용함을 보입니다. 이전에는 알아차리지 못한 이러한 통일성은 흥미로운 사실을 암시하는데, 이는 조금 이따가 다루겠습니다.
먼저 f를 원본 예측 모델(original prediction model)이라고 하고, g를 explanation model이라고 합니다. 여기서는 LIME에서 제안한 대로 하나의 입력 x에 대한 예측 f(x)를 설명하기 위해 서 설계된 local methods에 집중하겠습니다. 설명 모델(explanation model)은 흔히 단순화된 입력(simplified inputs) x′을 사용하는데, 이는 매핑 함수(mapping function) x=hx(x′)를 통해 원본 입력이 됩니다. Local methods는 z′≈x′일 때면 항상, g(z′)≈f(hx(z′))임을 보장하고자 합니다. 여기서 x′이 x보다 적은 정보를 포함할 수 있음에도 불구하고 hx는 현재의 입력 x에 한정되므로(specific to current input) hx(x′)=x입니다.
Definition 1
Additive feature attribution methods는 이진 변수의 선형 함수에 대한 설명 모델입니다.

여기서 z′∈{0,1}M이고, M은 단순화된 입력 특성(simplified input features)의 개수이며, ϕi∈R입니다. 이진 변수에 대한 함수이므로 z′은 0 또는 1입니다. 그리고 각 변수는 여러 개의 특성을 가질 수 있기 때문에 M번 곱해집니다. 예를 들어서, 세 개의 특성을 갖는다면 {1,0,1},{0,1,0}과 같은 값이 가능할 것입니다. Definition 1을 만족하는 설명 모델을 갖는 방식은 각 특성에 중요도(effect) ϕi를 부여하고 모든 특성의 중요도를 합하여 원본 모델의 출력 f(x)에 근사합니다. 많은 기존 방식들이 Definition 1을 만족하는데, 이에 대해 설명해보겠습니다.
2.1 LIME
LIME은 주어진 예측 주변에 대해 지역적으로 근사한 모델에 기반하여 각 모델 예측을 해석하는 방법입니다. LIME이 사용하는 local linear explanation model은 (1)번 수식을 정확히 준수하므로 additive feature attribution methods입니다. LIME에서 단순화된 입력 x′은 해석 가능한 입력(interpretable inputs)이라고 부르고, 매핑 x=hx(x′)은 interpretable inputs의 바이너리 벡터를 원본 입력 공간(original input space)으로 변환합니다. 서로 다른 입력 공간에 데해서는 서로 다른 형태의 hx 매핑이 사용됩니다. Bag of words 텍스트 특성에 대해서 hx는 여러 개의 1 또는 0(있거나 없거나)로 이루어진 벡터를 만약 simplified input이 1이면 원본 단어의 카운트로, 0이면 0으로 변환합니다. 이미지에서는 hx는 이미지를 super pixel의 집합으로 생각합니다. 그리고 1은 원본 값을 유지하는 것으로, 0은 이웃하는 픽셀의 평균값으로 대체하는 것으로 매핑합니다.
ϕ를 찾기 위해서, LIME은 다음과 같은 목적 함수를 최소화합니다.

설명 모델 g(z′)의 원본 모델 f(hx(z′))에 대한 충실도(faithfulness)는 로컬 커널 πx′에 의해 가중치가 부여된 단순화된 입력 공간의 샘플 집합에 대한 손실 L을 통해 강화됩니다. Ω는 g의 복잡도(complexitiy)에 대해 벌점을 부여하는 규제의 역할을 합니다. LIME에서 g는 (1)번 수식을 따르고 L은 제곱된 손실(squared loss)이므로 (2)번 수식은 penalized linear regression을 사용하여 풀 수 있습니다.
2.2 DeepLIFT
DeepLIFT는 당시 제안된지 얼마 되지 않은 재귀적 예측 설명 방법(recursive prediction explanation method)입니다. DeepLIFT는 각 입력 xi에 원래 값을 대신하여 대한 참조 값(reference value)을 사용하였을 때의 효과를 나타내는 값 CΔxiΔy을 할당합니다. DeepLIFT에서 매핑 x=hx(x′)은 이진 값을 원본 입력으로 변환하는데, 여기서 1은 원래 값을 취함을 나타내고, 0은 참조값을 취함을 의미합니다. 사용자에 의해 결정된 참조값은 특성에 대한 정보가 없는 값을 사용합니다. DeepLIFT는 다음과 같이 summation-to-delta 속성을 사용합니다.

o=f(x)는 모델의 출력을, Δo=f(x)−f(r),Δxi=xi−ri이며, r은 참조 입력을 의미합니다. ϕi=CΔxiΔo, ϕ0=f(r)이라고 하면, 아래 수식과 같이 DeepLIFT의 설명 모델은 (1)번 수식과 일치하며, 또 다른 additive feature attribution method가 됩니다.

2.3 Layer-Wise Relevance Propagation
Layer-wise relevance propagation은 심층 신경망의 예측을 해석하는 방법입니다. Shrikumer의 연구에서 언급되었듯이 이 방법은 모든 뉴런의 reference activations가 0으로 고정된 DeepLIFT와 동일합니다. 따라서 x=hx(x′)은 이진 값을 원본 입력 공간으로 변환하며, 1은 입력이 원본 값을 취함을, 0은 입력으로 0을 취함을 의미합니다. Layer-wise relevance progation의 설명 모델은 DeepLIFT와 같이 (1)번 수식과 일치합니다.
2.4 Classic Shapley Value Estimation
앞서 언급한 세 가지 방법은 cooperative game theory의 Shapley regression values, Shapley sampling values, Quantitative Input Influence와 같이 전통적인 방정식을 사용하여 모델 예측의 설명을 계산합니다.
Shapley regression values는 다중공선성이 존재하는 선형 모델의 특성 중요도입니다. 이 방법을 사용하기 위해서는 모든 특성(features)의 하위 집합 S⊆F에 대해 모델을 재학습해야 합니다. 여기서 F는 모든 특성의 집합입니다. 각 특성에 해당 특성을 포함하였을 때 모델 예측에 주는 영향을 나타내는 중요도를 할당합니다. 이 영향을 계산하기 위해서 모델 fS∪{i}는 그 특성을 포함하여 훈련되고, fS는 해당 특성을 제외하고 훈련합니다. 그리고 현재 입력에 대하여 두 모델의 예측을 비교하는데, 이를 fS∪{i}(xS∪{i})−fS(xS)와 같이 나타냅니다. 여기서 xS는 집합 S에 있는 입력 특성들의 값을 의미합니다. 어떤 특성을 제외할 때의 영향은 모델의 다른 특성에도 의존하기 때문에 이에 따른 차이는 모든 가능한 부분집합인 S⊆F ∖{i}에 대하여 계산됩니다. 그 후 shapley value를 계산하고 feature attribution으로 사용합니다. 이 값은 모든 가능한 차이(all possible differences)의 가중합이며, 수식은 다음과 같습니다.

Shapley regression value에서 hx는 1 또는 0을 원본 입력 공간으로 매핑합니다. 여기서 1은 입력이 모델에 포함됨을 의미하고, 0은 모델에서 제외됨을 의미합니다. 만약 ϕ0=f∅(∅) 라고 하면, Shapley regression values는 (1)번 수식과 일치하며 따라서 additive feature attribution method가 됩니다.
Shapley sampling values는 (1) sampling approximations(표푼 추출을 통하여 근사하는 방법)을 수식 (4)에 적용하고, (2) 학습 데이터 세트의 샘플을 합하여 모델에서 변수를 제거했을 때의 효과를 근사합니다. 이 방법은 모델을 재학습할 필요를 없애고 2|F| 보다 적은 차이(어떤 특성을 포함할 때와 포포함하지 않을 때)를 계산할 수 있게 해줍니다. Shapley sampling values의 설명 모델이 갖는 형식이 Shapley regression values와 같기 때문에 이는 또 다른 additive feature attribution method입니다.
Quantitave input influence는 feature attribution보다 더 넓은 범위를 다루는 네트워크입니다. 하지만 이 방법의 일부로 Shapley sampling values와 거의 동일한 Shapley values에 대한 sampling approximation을 독립적으로 제안합니다. 따라서 이것 또한 additive feature attribution method가 됩니다.
3. Simple Properties Uniquely Determine Additive Feature Attributions
Additive feature attribution methods 클래스의 놀라운 특성은 세 개의 desirable properties를 갖는 유일해(single unique solution)가 존재한다는 것입니다. 이러한 특징은 Shapley value estimation methods에 대해서는 익숙하지만, 다른 접근법에 대해서는 잘 알려지지 않았었습니다.
첫 번째 desirable property는 local accuracy입니다. 원본 모델 f를 특정한 입력 x에 대하여 근사했을 때, local accuracy는 설명 모델이 단순화된 입력 x′이 f의 출력과 일치할 것을 요구합니다.
Property 1 (Local accuracy)

x=hx(x′)일 때, 설명 모델 g(x′)은 원본 모델 f(x)와 일치합니다.
두 번째 특징은 missingness입니다. 만약 단순화된 입력이 특성의 존재 여부를 의미한다면, missingness는 생략된 특성(feature missing)이 원본 입력에 영향을 미치지 않을 것을 요구합니다. 2절에서 언급한 모든 방법은 이 특징을 만족합니다.
Property 2 (Missingness)

Missingness는 x′=0인 특성이 어떠한 영향도 미치지 않도록 억제합니다.
세 번째 속성은 consistency입니다. Consistency는 어떤 모델이 변형되어 다른 입력과 관계없이 일부 단순화된 입력의 영향(contribution)이 증가하거나 그대로 유지된다면, 해당 입력의 중요도(attribution)이 감소하지 않아야 한다는 것을 의미합니다.
Property 3 (Consistency)
fx(z′)=f(hx(z′))이고 z′ ∖i가 z′i=0을 나타낸다고 하고, 임의의 두 모델 f와 f′이 모든 입력 z′∈{0,1}M에 대하여 다음 조건을 만족한다고 가정하겠습니다.
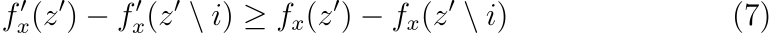
그러면 ϕi(f′,x)≥ϕi(f,x)입니다.
Theorem 1
Definition 1을 따르고 Properties 1, 2, 3을 만족하는 설명 모델 g은 오직 한 개만 존재할 수 있습니다.

여기서 |z′|은 z′에서 0이 아닌 값의 개수를 의미하고, z′⊆x′은 0이 아닌 값이 x′의 0이 아닌 값의 부분집합인 모든 z′ 벡터를 의미합니다.
Theorem 1은 combine cooperative game theory의 결과를 따르고, ϕi는 Shapley values로 알려져 있습니다. Young은 Shapley values가 Property 1, 3과 비슷한 세 개의 공리를 따르는 유일한 집합임을 증명하였습니다. Property 2는 Shapley 증명을 additive featur attribution methods 클래스에 적용하는 데 필요합니다.
단순화된 입력 매핑 hx가 주어졌을 때, Property 1-3에 의해 Theorem 1은 가능한 additive feature attribution method가 유일함을 증명합니다. 이는 Shapley values에 기반하지 않은 방법은 local accuracy와 consistency 중 하나 또는 모두를 위반함을 의미합니다. Missingness는 모든 방법들에서 만족됨을 이미 확인하였습니다.
4. SHAP (SHapley Additive exPlanation) Values
여기서는 의도치 않게 Properties 1, 3을 위반하는 것을 방지하여, 이전에 언급한 방법들을 개선한 통합된 방법을 제안합니다.
SHAP은 특성 중요도를 측정할 통합 지표입니다. 이는 원본 모델에 대한 Shapley value의 조건부 기댓값 함수입니다. 따라서 이 방법은 수식 (8)의 해가 됩니다. fx(z′)=f(hx(z′))=E[f(z)|zS]일 때 S는 z′에서 0이 아닌 값의 인덱스의 집합입니다. SHAP value의 정의는 단순화된 입력 매핑 hx(z′)=zS를 의미하고, zS는 집합 S에 속하지 않은 특성에 대한 missing values를 갖습니다. 대부분의 모델은 생략된 입력에 대한 임의의 패턴을 다루지 못하기 때문에, f(zS)를 E[f(z)|zS]로 근사하였습니다. SHAP value의 이 정의는 Shapley regression, Shapley sampling, quantitative input influence feature attribution을 서로 밀접하게 연관짓고(closely align), LIME, DeepLIFT와 layer-wise relevance propagation과의 연결 또한 가능하게 하기 위하여 설계되었습니다.
SHAP value를 정확하게 계산하는 것은 어렵습니다. 하지만 현재 알고 있는 additive feature attribution methods에서 얻은 인사이트를 합하여 근사할 수는 있습니다. 저자는 두 개의 어떤 모델에든 적용할 수 있는 근사법을 설계하였는데, 하나는 이미 알려진 Shapley sampling values이고 다른 하나는 새로운 방법인 Kernel SHAP입니다. 또한 모델에 따라서 다르게 사용할 수 있는 네 개의 근사법을 소개하였는데, 그 중 두 개는 Max SHAP와 Deep SHAP입니다. 이러한 방법을 사용할 때 특성의 독립성과 모델의 선형성은 기대값을 계산하는 과정을 단순화하는 두 가지 최적의 가정입니다.

4.1 Model-Agnostic Approximations
조건부 기대값을 근사할 때 feature independence를 가정한다면, SHAP value는 Shapley sampling values나 Quantitative Input Influence를 사용하여 직접 측정할 수 있습니다. 이 방법은 전통적인 Shapley value equations (수식 (8))의 sampling approximation을 사용합니다. 개별 샘플 추정(separate sampling estimates)을 각 특성 중요도에 대하여 수행됩니다. 적은 숫자의 입력에 대해서 계산하는 것이 합리적이지만 Kernel SHAP는 유사한 근사 정확도를 얻기 위해서 원본 모델에 대한 평가 횟수를 더 적게 요구합니다.
Kernel SHAP (Linear LIME + Shapley values)
Linear LIME은 선형 설명 모델을 사용하여 f를 지역적으로 근사합니다. 여기서 local은 단순화된 이진 입력 공간에 대하여 측정합니다. 여기서 수식 (2)의 해가 원래 값을 복구할 수 있는지가 중요합니다. 정답은 손실 함수 L과 weighting kernel π′x, 그리고 규제 항 Ω를 어떻게 정의하느냐에 따라 다르다입니다. LIME에서 이 파라미터를 선택하는 것은 휴리스틱하게 이루어집니다. 그런데 이러한 방법으로는 수식 (2)가 Shapley values를 복원할 수 없습니다. 그 결과로 local accuracy나 consistency 둘 중 하나 또는 모두가 위반되고, 특정 상황에서 의도하지 않은 행동을 하게 결과를 낳을 수도 있습니다. 다음은 휴리스틱하게 파라미터를 결정하는 대신 Shapley values를 복원할 수 있도록 값을 결정하는 방법입니다.
Theorem 2 (Shapley Kernel)
Definition 1에 의해 수식 (2)의 해를 만족하고 Properties 1, 3을 만족하는 π′x, L, Ω는 다음과 같습니다.

여기서 |z′|은 z′의 0이 아닌 원소의 개수를 의미합니다.
4.2 Model-Specific Approximations
Kernel SHAP가 모델과 관계없이 적용 가능한 SHAP value의 측정 방식의 효율성을 개선하였다면, 특정한 모델로 한정한다면 더욱 빠른 근사법인 Linear SHAP을 사용할 수 있습니다.
Linear SHAP
선형 모델에 대해서 입력 특성의 독립을 가정한다면, SHAP values는 모델 가중치 계수로부터 직접적으로 근사할 수 있습니다.
Corollary 1 (Linear SHAP)
선형 모델 f(x)=∑Mj=1wjxj+b:ϕ0(f,x)=b가 주어 졌을 때, 다음 수식이 만족됩니다.

Low-Order SHAP
Theorem 2를 사용하는 선형 회귀는 O(2M+M3)의 복잡도를 갖기 때문에 M의 값이 작을 때 효율적입니다.
Max SHAP
Permuation formulation of Shapley values를 사용하여 각 입력이 다른 모든 입력보다 최댓값을 증가시킬 확률을 계산할 수 있습니다. 입력의 정렬 순서대로 이 작업을 수행하면 O(M2M)이 아닌 O(M2) 시간 내에 M개의 입력을 갖는 Shapley values의 최대 함수를 계산할 수 있습니다.
Deep SHAP (DeepLIFT + Shapley values)
Kernel SHAP는 심층 신경망을 포함한 어떤 모델에서든 사용할 수 있지만, 심층 신경망의 구성의 특징에 대한 추가적인 정보를 활용하여 계산 성능을 개선할 수 있는 방법이 있는지 확인해보아야 합니다. 저자는 이 문제에 대하여 이전에는 알려지지 않은 Shapley values와 DeepLIFT의 관계를 통해 답을 찾았습니다. 수식 (3)의 reference value를 수식 (12)의 E[x]로 나타내면, DeepLIFT는 입력 특성이 서로 독립적이며 deep model이 선형임을 가정하여 SHAP values를 근사합니다. DeepSHAP는 휴리스틱하게 linearize components를 선택할 필요를 없애주는 대신, 효과적인 선형화를 유도합니다.
5. Computational and User Study Experiments
저자는 Kernel SHAP과 Deep SHAP를 사용하여 SHAP values의 효용을 측정하였습니다. 먼저 Kernel SHAP과 LIME의 연산 효율과 정확성을 비교하였고, SHAP values와 DeepLIFT, LIME과 같은 다른 특성 중요도 할당 방법을 비교하는 user study를 설계하였습니다.
Theorem 2는 게임 이론에서 유래한 Shapley value와 가중 선형 회귀를 연결합니다. Kernel SHAP은 이를 통해 특성 중요도를 계산합니다. 이 방법은 원본 모델에 대한 더 적은 검증을 바탕으로 더 정확한 측정이 가능하게 합니다. 특히 선형 모델에 규제가 추가된 경우에는 이 효과가 더욱 극대화됩니다.
저자는 LIME, DeepLIFT, SHAP을 Amazon Mechanical Turk를 사용하여 단순한 모델에 대한 유저의 설명과 비교하였습니다. 이 실험은 좋은 모델 설명은 모델을 이해한 사람의 설명과 일치해야함을 전제로 하였습니다. 두 가지 세팅에서 실험을 진행하였는데, 첫 번째는 두 증상 중 하나만 나타날 경우 고통 점수(sickness score)가 높은 상황입니다. 두 번째는 DeepLIFT가 적용될 수 있는 최대 할당(max allocation) 문제입니다. 참가자는 세 사람이 받은 점수 중 최고점에 기반하여 돈을 얻는 방법에 대한 짧은 스토리를 듣습니다. 두 경우에서 참가자는 입력에 대한 출력에 점수를 할당합니다. 그리고 다음과 같이 사람의 설명은 SHAP의 결과가 다른 모델보다 더욱 일치하는 것을 알 수 있습니다.

6. Conclusion
모델 예측의 정확성과 해석 가능성 사이의 균형에 대한 관심이 커지면서 사용자가 예측을 해석하는 방법도 발전하였습니다. SHAP 프레임워크는 additive feature importance methods 클래스를 정의하고 desirable properties를 갖는 유일해가 존재함을 입증하였습니다. SHAP은 모델 해석에 대한 일반적인 원칙을 제시하고 향후 연구되는 방법에 대한 발전 가능성을 제시합니다.
7. Further thinking
데이터 분석 대회 중 각 입력 특성이 타겟에 미치는 영향을 분석하고, 불필요한 특성을 제거할 필요가 있었습니다. 이 과정에서 SHAP에 대해서 알게 되어 논문을 읽어보았습니다. 수식과 요구하는 배경지식이 매우 많아서 정말 이해하기 어려웠고, 다 읽고 리뷰를 했음에도 불구하고 진짜로 내 것이 되었는지에 대해서는 그렇다고 답을 하지 못할 것 같습니다. 다만 SHAP value가 어떤 의미를 갖고, 어떤 의도로 설계되었는지에 대해서만 어렴풋이 알게 되었습니다. 조사하던 중 이 개념이 XAI(Explainable AI) 분야의 내용임을 알게 되었습니다. 딥러닝은 블랙박스라는 말이 만연하면서, XAI에 대해 관심가진 적이 있었는데, 제대로 공부해본 적은 없습니다. 그런데 우연히 읽은 논문이 해당 분야의 것임을 알게되었고, 생각보다 정말 중요하고 또 어려운 분야라는 것을 깨달았습니다. XAI에 대하여 제대로 공부하게 된다면 여기서 언급된 LIME, DeepLIFT등에 대해서도 알아보고 수식을 다시 한번 뜯어보고 싶다는 생각이 들었습니다.




댓글