
Static Embedding과 비교하여 Contextualized representations가 어떤 특징을 갖는지에 대해 분석한 논문인 How Contextual are Contextualized Word Representations? Comparing the Geometry of BERT, ELMo, and GPT-2 Embeddings를 리뷰해보았습니다. 이번 논문은 이해하기가 특히 어렵고, 한글로 옮기기 어려운 개념들이 많았던 것 같습니다. 번역을 통해 오히려 이해가 어려워지거나, 원문의 표현을 사용하는 게 원래 의미를 온전히 잘 전달할 것이라고 생각하는 표현은 원문의 표기를 따랐습니다. 오개념이나 오탈자가 있다면 댓글로 지적해주세요. 설명이 부족한 부분에 대해서도 말씀해주시면 본문을 수정하겠습니다.
Overview
단어를 저차원의 연속 공간(low-dimensional continuous space) 내에 있는 벡터로 표현하는 방법 덕분에 자연어 처리 문제를 딥러닝으로 해결할 수 있게 되었습니다. 원래 이런 단어 임베딩(word embedding)은 정적 임베딩이었습니다. 문맥에 무관하게 각 단어는 동일한 벡터로 표현되었습니다. 하지만 이러한 방식은 몇 가지 문제점이 있는데, 가장 주요한 것은 다의적(polysemous)인 어휘도 같은 벡터 표현만을 사용해야 한다는 점입니다. ELMo나 BERT와 같은 모델들은 문맥에 따른 단어 표현(contextualized word representations)을 성공적으로 제공하여, 단어가 등장하는 문맥에 따라 다양한 벡터 표현을 생성할 수 있게 되었습니다. 질문 답변부터 상호참조해결 문제에 이르기까지 NLP 분야의 다양한 태스크에선 정적 임베딩 대신 contextualized representation를 사용하여 눈에 띄는 성능 개선이 이루어졌습니다.
문맥에 맞는 단어 표현의 큰 성공은 language modelling task로만 학습되어도, 모델이 전이할 수 있고(transferable) 작업에 구애받지 않는 성질을 갖게 되었음을 의미합니다. 실제로 frozen contextualized representations으로 훈련된 linear probing model 또한 단어의 언어적 특성을 잘 예측합니다. 하지만 여전히 이러한 벡터 표현들은 문맥에 대한 이해도가 부족합니다. 그러면 contextualized word representations은 얼마나 문맥을 잘 이해하고 있을까요? BERT와 ELMo가 각 단어에 할당할 수 있는 문맥을 고려한 벡터는 무한히 많을까요? 아니면 한정된 개수 중에서 하나를 골라서 할당해주는 것일까요? 저자는 ELMo, BERT 그리고 GPT-2 모델의 각 레이어가 갖는 벡터 표현 공간의 기하적 특성을 탐구하여 이 질문에 대한 답을 탐구했습니다. 그리고 다음과 같은 놀라운 사실들을 발견했습니다.
먼저, 세 모델의 모든 레이어에서 contextualized word representations은 등방성을 갖지 않습니다(not isotropic). 즉 각 방향에 대해 균일하게 분포해있지 않습니다. 대신 그들은 앞서 언급했던 등방성을 갖지 않고(anisotropic) 좁은 콘 모양의 공간을 차지합니다. GPT-2의 마지막 레이어는 anisotropy가 극심해서 심지어는 임의로 선택한 두 단어의 코사인 유사도의 평균이 거의 1에 가까울 정도입니다. 이전 연구에서는 정적 임베딩이 등방성(isotropy)을 가질 때 유리하다는 것이 이론적, 실험적으로 밝혀졌는데, 이에 비해 contextualized representations의 이러한 높은 비등방성(anisotropy)은 놀라운 결과입니다.
서로 다른 문맥에서 나타나는 동일한 단어는 같지 않은 벡터 표현을 갖습니다. 코사인 유사도로 벡터의 유사도를 정의하는데, 모델의 상위 레이어로 갈수록 이 유사도는 더욱 낮아집니다. 이는 모델의 상위 레이어로 갈수록 문맥에 따른 의미가 더 많이 담긴 벡터 표현이 만들어짐을 의미합니다.
맥락에 따른 특성(context-specificity)는 ELMo, BERT, GPT-2에서 모두 다르게 나타납니다. ELMo는 context-specificity가 상위 레이어로 갈수록 증가하면서 같은 문장에 있는 단어들의 벡터는 점점 더 유사해집니다. BERT에서는 반대로 상위 레이어로 갈수록 같은 문장 내 단어의 벡터끼리의 유사도가 낮아집니다. 그래도 임의로 선택된 두 단어보다는 같은 문장 내의 두 단어의 유사도가 더 높습니다. 하지만 GPT-2에서는 같은 문장 내 두 단어의 유사도가 임의로 선택한 두 단어의 유사도보다 높지도 않습니다.
Anisotropy의 영향을 조절한 다음, 평균적으로 contextualized representations의 첫번째 주성분(first principal component)은 분산의 5% 미만밖에 설명하지 못합니다. 이는 모든 모델의 모든 레이어에 적용됩니다. 이 사실은 contextualized representations가 유한한 단어 벡터(word-sense vector)에 대응되지 않는다는 것을 의미하고 가장 최선의 시나리오에서조차 정적 임베딩은 contextualized 임베딩보다 좋지 못하다는 것을 의미합니다. 실제로 contextualized representations의 첫 번째 주성분을 이용해 정적 임베딩을 생성하면, 여러 단어 벡터 벤치마크에서 GloVe나 FastText 임베딩보다 더 우수한 성능을 보였습니다.
이러한 사실들은 어떻게 contextualized representations가 NLP의 여러 태스크에서 눈에 띄는 성능 향상을 불러왔는지에 대해서 알 수 있게 해줍니다.
Approach
Contextualized Models
논문에서 사용된 모델은 ELMo, BERT, GPT-2입니다. BERT는 base cased 버전을 사용하였는데, 이는 GPT-2와 레이어의 수와 벡터의 차원이 유사하기 때문입니다 . 각 모델은 각자의 방식대로 사전훈련된 상태입니다. ELMo는 2개, BERT와 GPT는 12개의 레이어를 갖지만 저자는 입력층을 0번째 레이어로 정의하였습니다. 0번째 레이어는 contextualized가 이루어지지 않았기 때문에, 후속 레이어에서 contextualized된 정도를 비교하는 좋은 베이스라인이 될 수 있기 때문입니다.
Data
SemEval Semantic Textual Similarity 태스크에서 사용한 데이터를 사용하였습니다. 이 데이터셋은 서로 다른 문맥에서 등장하는 같은 단어에 대한 문장을 포함합니다. 논문에서는 dog이라는 단어가 등장하는 두 문장, “A panda dog is running on the road.”와 “A dog is trying to get bacon off his back.”을 예시로 보여줍니다. 만약 모델이 dog에 대한 같은 벡터 표현을 생성한다면 contextualization이 이루어지지 않았음을 추론할 수 있고, 반대로 서로 다른 벡터가 생성된다면, contextualized가 어느 정도 이루어졌다고 생각할 수 있습니다.
Measures of Contextuality
단어의 표현이 얼마나 문맥을 잘 이해하는지는 다음 세 가지 지표를 사용하여 측정합니다.
Self-similarity
w는 문장 s1,…,sn 각각에서 i1,…,in번째 인덱스에 등장한다고 하겠습니다. 예를 들어서 s1[ii=5]라면 단어 w는 첫 번째 문장의 5번째 단어에 해당합니다. 위와 같이 정의하면 w=s1[i1]=⋯=sn[in]임을 알 수 있습니다. 이제 fℓ(s,i)를 모델 f의 ℓ번째 레이어에서 s[i]가 대응하는 벡터 표현에 매핑되는 함수라고 정의합니다. 그러면 self similarity는 다음과 같이 정의됩니다.

수식을 한 번에 이해하기 어려우니 단계별로 설명해보겠습니다. 먼저 j는 고정한 상태에서 두 번째 ∑안쪽부터 살펴보죠. cos는 코사인 유사도를 계산하는 함수입니다. 모델과 레이어는 f와 ℓ로 고정된 상태입니다. 나머지를 보면, j번째 문장의 단어 w에 대한 벡터와 j가 아닌 다른 모든 문장의 단어 w에 대한 벡터의 코이산 유사도를 계산한다는 의미입니다. ∑ 기호가 하나 더 있는데, 앞에서는 문장 하나를 고정시킨 후 생각했지만, 이제 단어 w를 갖는 모든 문장을 서로 비교하겠다는 의미입니다. 그리고 마지막으로 n2−n으로 나누어 평균을 구합니다. 쉽게 말해서 같은 단어가 여러 개의 문장에서 각각 서로 다른 벡터로 매핑되었을텐데, 그 벡터들간의 유사도를 모두 비교한다는 의미입니다. 논문의 표현을 빌려 조금 더 기술적으로 말하면, 단어 w에 대해 n개의 unique contexts에서 각각 들어진 contextualized representations끼리의 코사인 유사도의 평균을 계산합니다.
만약 레이어 ℓ이 contextualize되지 않았다면 SelfSimℓ(w)=1일 것입니다. 즉 모든 문맥에서 단어의 벡터가 동일할 것입니다. 단어 w에 대해 더 많이 contextualized될수록 self-similarity의 값은 작아질 것입니다.
Intra-sentence Similarity
s는 n개의 단어 ⟨w1,…,wn⟩로 이루어진 문장이라고 하겠습니다. fℓ(s,i)은 self-similarity에서 정의한 것과 같습니다. 그러면 intra-sentence similarity는 다음과 같이 정의할 수 있습니다.

먼저 수식에서 where 다음 부분의 문장에 대한 벡터 표현이 어떻게 만들어지는지를 보겠습니다. 여기서 주의할 점은 i에 밑첨자가 없습니다. 즉 문장에 있는 모든 단어들에 대한 벡터 표현을 만들어서 합한 후 단어의 개수인 n으로 나누어줍니다.
이제 IntraSim은 어떻게 계산되는지 보겠습니다. 앞에서 만든 문장에 대한 벡터 표현과 문장에 있는 각 단어의 벡터 표현끼리의 코사인 유사도를 계산한 후 모두 합하고 단어의 개수인 n으로 나누어줍니다. 쉽게 생각하면 전체 문장과 문장 내 각 단어가 문맥적으로 어느 정도의 유사도를 갖는지를 계산한다는 의미입니다. 이는 벡터 공간에서 context-specificity가 얼마나 잘 나타나는지를 보여줍니다. 예를 들어서 IntraSimℓ(s)와 SelfSimℓ(w)가 문장 s안에 있는 모든 단어 w에 대해 낮다면, 모델의 해당 레이어가 각 문장의 문맥도 구분하면서, 각 단어에 대해서도 문맥에 따른 벡터 표현을 만들어줌을 의미합니다. 만약 IntraSimℓ(s)은 높지만 SelfSimℓ(w)가 낮다면, 모델이 각 단어에 대한 문맥을 단순히 같은 문장 안에 있으면 유사한 의미를 갖는다는 식으로만 학습한다는 것을 의미합니다.
Maximum Explainable Variance
MEVℓ(w)는 레이어 ℓ에서 w의 contextualized representations이 첫 번째 주성분으로 설명될 수 있는 분산의 비율을 의미합니다. 다시 말해서, MEV는 각 단어의 contextualized 벡터 표현들의 주성분 분석을 통해 첫 번째 주성분이 전체 분산 중 얼마만큼을 설명하는지를 나타내는 지표입니다. 레이어 ℓ의 단어 w에 대한 벡터 표현들을 행렬로 나타낸 것 [fℓ(s1,i1)…fℓ(sn,in)]을 occurence matrix라고 하겠습니다. σ1…σm을 이 행렬의 처음 m개의 특이값(singular value)라고 하면, MEVℓ(w)maximum explainable variance는 다음과 같이 정의할 수 있습니다.
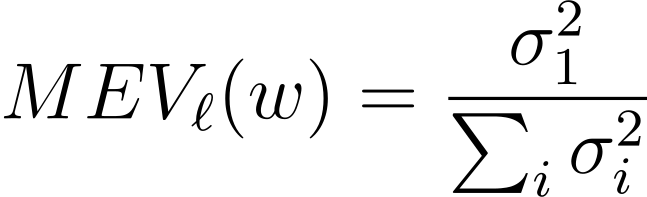
이 지표는 단어 w의 벡터 표현들 중 가장 중요한 성분이 얼마나 많은 정보를 포함하고 있는지를 나타냅니다. 즉, 정적 임베딩이 contextualized representations을 어느 정도 수준까지 대체할 수 있는지에 대한 상한선을 알려줍니다. MEVℓ(w)가 낮다면 해당 단어의 정보는 여러 성분에 걸쳐 분산되어 있으므로, 이를 사용한 정적 임베딩의 성능은 좋지 않을 것입니다. 반대로 이 값이 높다면 단어의 정보가 하나의 벡터에 대부분 담겨있으므로, 이를 사용한 정적 임베딩은 contextualized representations을 잘 대체할 수 있을 것입니다.
Adjusting for Anisotropy
Contextuality는 istotropy와 함께 고려되어야 합니다. 예를 들어, 단어 벡터들이 완벽하게 등방성(isotropic)을 가질 때, SelfSimℓ(w)=0.95는 w의 벡터 표현이 문맥에 따라 다르게 표현되지 않았다는 것을 의미합니다. 하지만 단어 벡터들이 매우 높은 비등방성(anisotropic)을 갖고, 임의의 두 단어의 코사인 유사도가 0.99라면, SelfSimℓ(w)=0.95은 w의 벡터 표현이 문맥에 따라 다르게 표현되었음을 의미합니다. 서로 다른 문맥에서 등장한 w의 벡터간의 코사인 유사도는 임의의 두 단어 간의 코사인 유사도보다 낮기 때문입니다.
Anisotropy의 영향을 조정하기 위해서, 저자는 세 가지 anisotropic baseline을 사용하였습니다. Self-similarity와 intra-sentence similarity에서 사용한 베이스라인은 서로 다른 문맥에서 나타나는 두 단어 간의 코사인 유사도의 평균입니다. 주어진 레이어에서 벡터 표현의 비등방성이 더욱 높을수록 베이스라인의 값은 1에 가깝습니다. Maximum Explainable Variance에서 사용한 베이스라인은 균일 분포에서 임의로 추출한 단어의 벡터 표현에 대한 PCA를 수행하고, 첫번째 성분이 전체 벡터를 설명하는 비율의 평균입니다. 이 베이스라인의 값이 1에 가까울수록, 임의의 단어를 선택해도 그 단어 벡터의 주성분이 전체 분산의 대부분을 설명할 수 있을 것입니다.
Contextuality 지표들은 각 모델의 모든 레이어에서 측정되었기 때문에, 레이어마다 기준값(baseline)을 별도로 계산하였습니다. 그리고 각 지표의 값에서 그에 대응하는 기준값을 빼어 anisotropy-adjusted contextuality measure을 계산하였습니다. 예를 들어서 anisotropy-adjusted self-similarity는 다음과 같이 계산되었습니다.
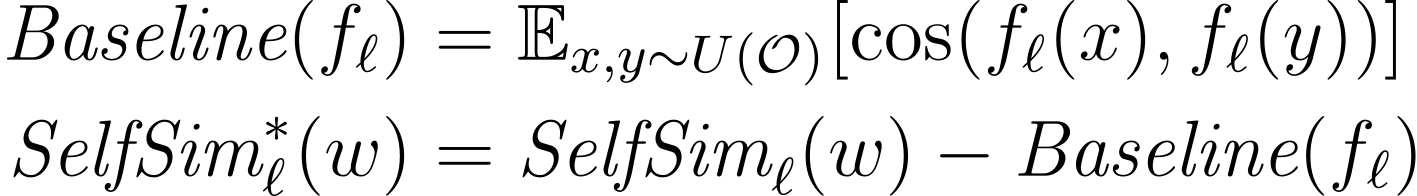
O는 관찰된 모든 단어의 집합을 의미하고, fℓ(⋅)은 모델 f의 레이어 ℓ에서 단어를 벡터 표현으로 매핑하는 함수입니다. 앞으로 특별한 언급이 없는 한 contextuality measures들은 이렇게 비등방성에 대해 조정된 지표라고 생각하겠습니다.
Findings
(An)Isotropy
입력층을 제외한 모든 레이어에서 contextualized representations은 비등방성을 갖습니다. 만약 특정 레이어에 있는 단어들의 벡터가 등방성을 갖는다면 균일분포에서 선택한 임의의 두 단어에 대한 코사인 유사도의 평균은 0일 것입니다. 이 값이 1에 가까울수록 비등방성이 높고, 단어 벡터는 좁은 콘 모양의 벡터 공간을 차지할 것입니다. 그리고 비등방성이 높을수록 콘의 모양은 더 좁아질 것입니다.
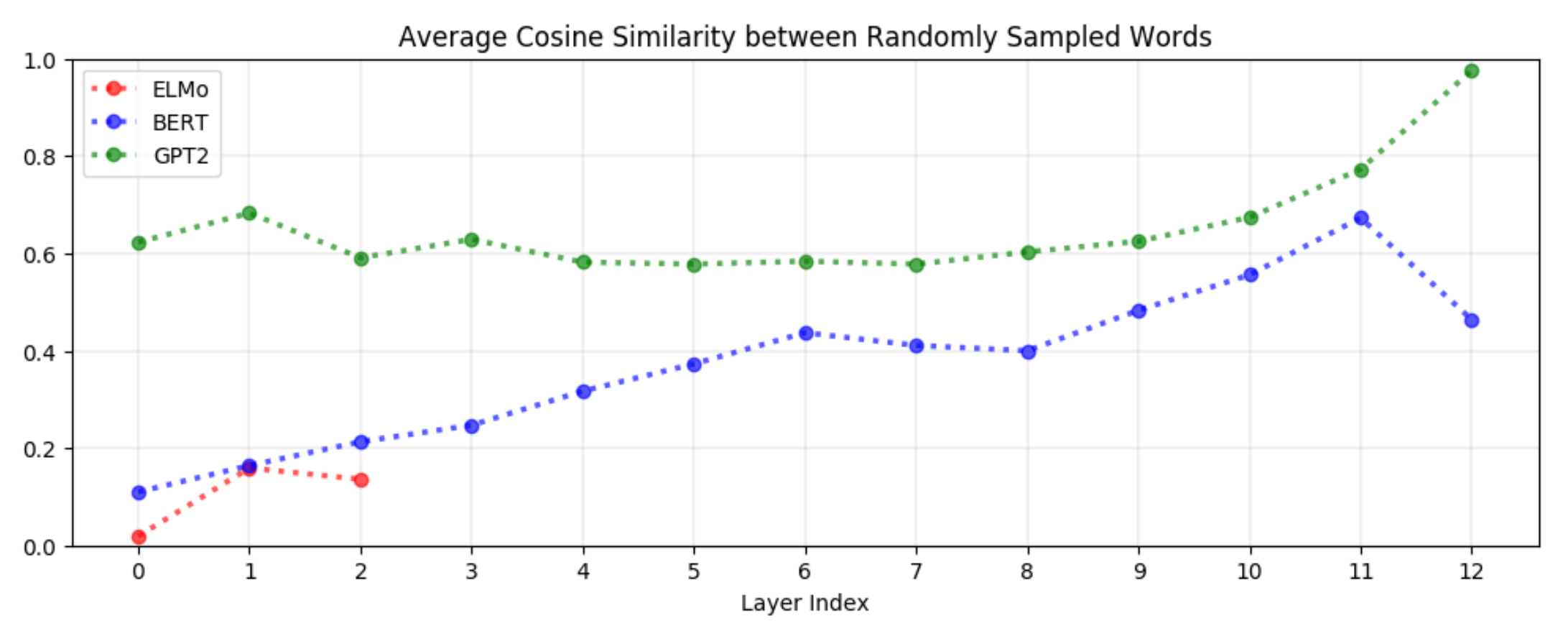
그래프와 함께 보면 BERT, ELMo, GPT-2의 모든 레이어에서 모든 단어의 벡터들은 좁은 콘 모양을 차지할 것임을 알 수 있습니다. Contextual, positional 정보를 전혀 사용하지 않고 글자 수준에서 정적 임베딩을 만드는 ELMo의 입력층만은 예외입니다. 물론, 모든 정적 임베딩이 isotropic한 것은 아닙니다.
Contextualized representations은 일반적으로 상위 레이어로 갈 수록 비등방성이 커집니다. 위의 그래프에서 알 수 있듯이, GPT-2는 2~8번째 레이어에서 임의의 두 단어 벡터의 코사인 유사도가 약 0.6 정도인데, 8~12번째 레이어에서는 그 값이 지수적으로 증가하는 것을 볼 수 있습니다. GPT-2의 마지막 레이어는 비등방성이 너무 높아서 코사인 유사도가 거의 1에 가까울 정도입니다. 예외는 있지만 이러한 패턴은 BERT나 ELMo에서도 비슷합니다. BERT는 마지막에서 두 번째(penultimate) 레이어에서 가장 높은 값을 가집니다. 앞서 언급했던 정적 임베딩에서 isotropy를 갖는다는 것은 이론적, 실험적으로 유용합니다. 이론적으로는, 등방성은 훈련 과정에서 self-normalization을 갖게 하므로 수렴 속도와 안정성 면에서 유리하고, 실제로 NLP의 여러 다운스트림 태스크에서도 성능 향상을 가져옵니다. 따라서 contextualized representations이 이 정도의 비등방성을 갖는 것은 놀랍습니다. 따라서 비등방성은 Contextualization의 내재된 특성이거나, 아니면 그 과정에서 발생하는 잔여물이라고 생각할 수 있습니다.
Context-Specificity
Contextualized word representations은 상위 레이어에서 더욱 context-specific해집니다. 즉, 상위 레이어에서 문맥에 대한 특성을 더 잘 이해합니다. 균일 분포에서 임의 추출한 두 단어의 평균 self-similarity에 대한 다음 그래프를 보겠습니다. 세 모델 모두에서 상위 레이어로 갈수록 self-similarity가 감소합니다. 즉 상위 레이어로 갈수록 단어 벡터가 문맥에 따른 특성을 더 많이 반영하게 됩니다. 이미지 분류 태스크에 비유하면, 하위 레이어에서는 일반적인 특성들을 파악하고, 상위 레이어에서 더 구체적인 특성을 관찰하는 것과 같습니다.
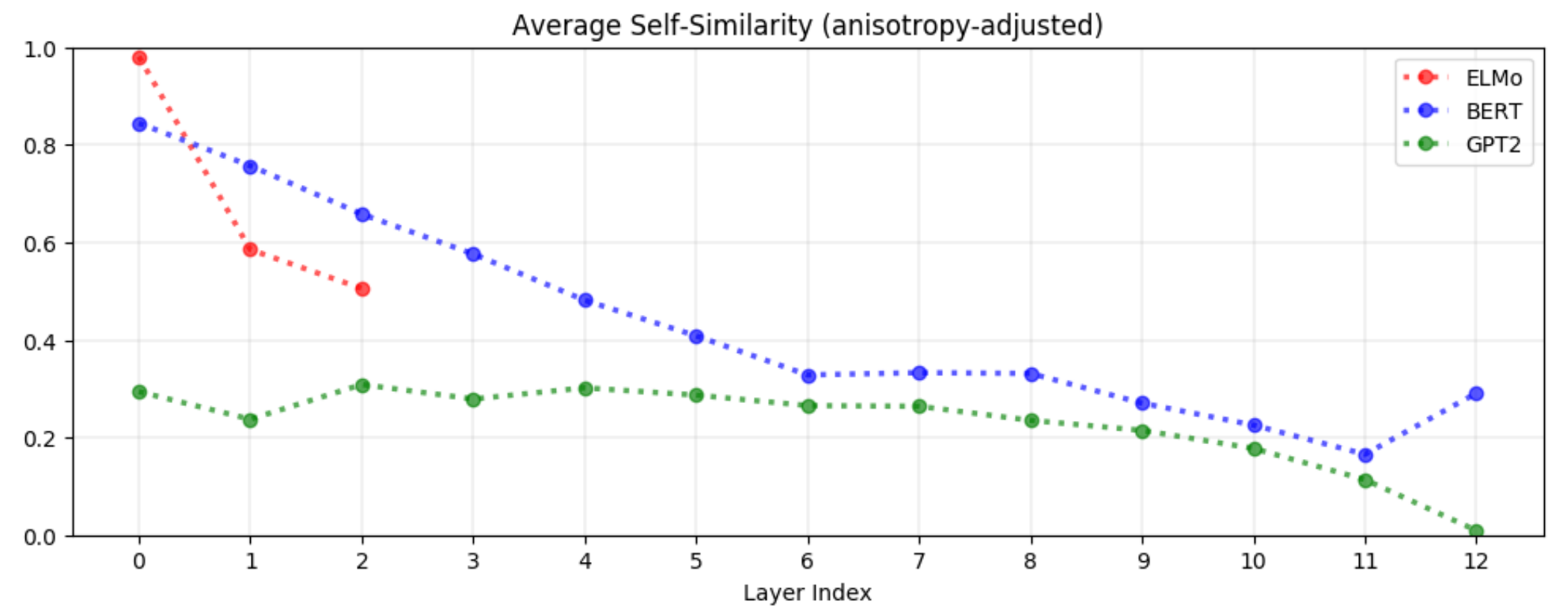
불용어(Stopwords; the, of, to 등)는 가장 큰 context-specific representations을 갖습니다. 모든 레이어에서 불용어는 가장 낮은 self-similarity를 보였습니다. 이런 단어들이 실제로 다양한 의미를 갖지는 않는다는 점을 생각하면 놀라운 결과입니다. 이는 단어에 내재된 다의성보다는 단어가 등장하는 문맥이 다양할수록 contextualized representations가 다양해진다는 것을 의미합니다. 이는 처음에 저자가 가졌던 의문에 대한 답을 제시합니다. 결국 ELMo, BERT, GPT-2는 각 단어에 유한한 숫자의 벡터 중 하나를 할당해주는 게 아니라, 각 단어에 대한 무한히 많은 벡터 표현이 존재할 수 있다는 것을 의미합니다.
Context-Specificity는 ELMo, BERT, GPT-2에서 모두 다르게 나타납니다. 앞에서는 세 모델 모두에서 상위 레이어로 갈수록 context-specificity가 높아진다고 하였습니다. 하지만 벡터 공간에서는 그 양상이 조금 다릅니다. 같은 문장 내의 단어 벡터는 한 점으로 모이게 될까요? 아니면 서로 멀어지긴 하지만 아예 다른 문장에서 나타난 단어들보다는 더 가까이 위치할까요? 이를 확인하기 위해서는 intra-sentence similarity를 살펴봐야 합니다.
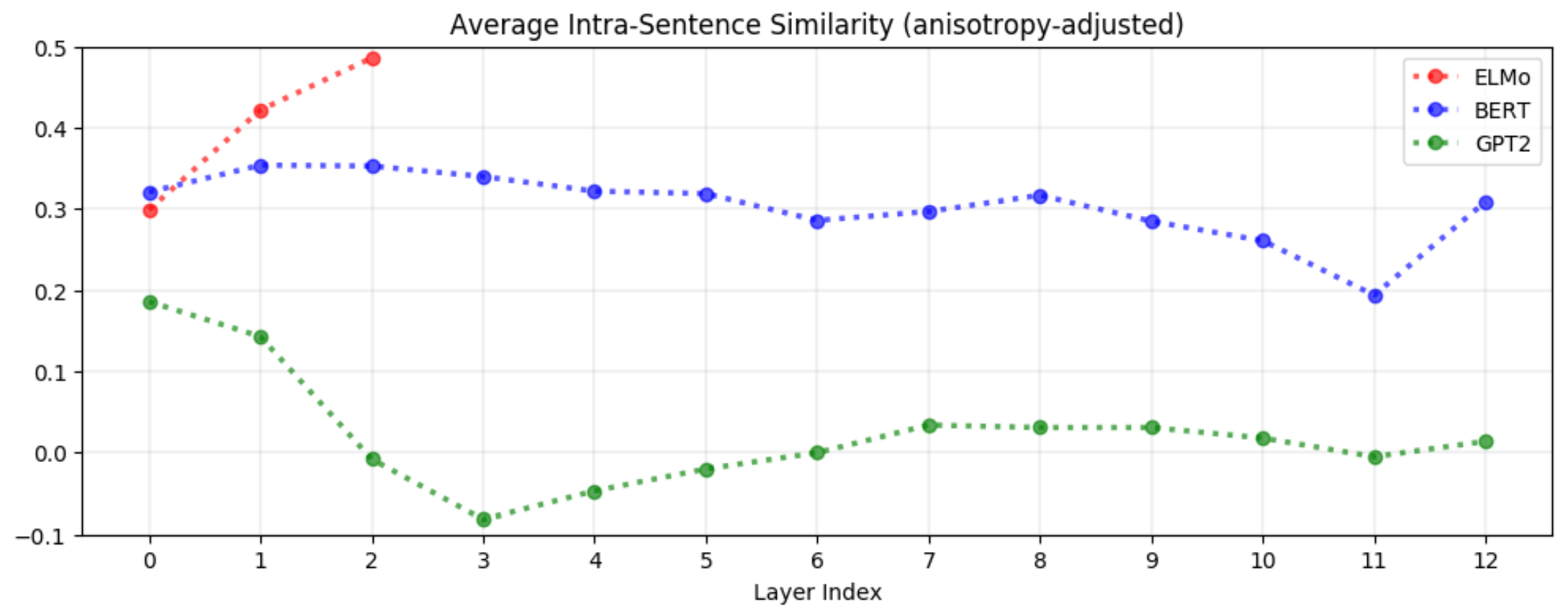
ELMo에서는 상위 레이어로 갈수록 같은 문장 안에 있는 단어들끼리는 유사도가 높아집니다. 이 사실은 결국 Firth가 수립한 분산 표현에 대한 가설인 동일한 문맥에서 등장한 단어들끼리의 contextualized representations은 서로 유사할 것이다가 참임을 입증합니다.
반대로 BERT는 상위 레이어로 갈 수록 같은 문장 안에 있는 단어들끼리의 유사도가 낮아집니다. 마지막 레이어는 예외이지만, 상위 레이어로 갈수록 문맥에 특화된 정보를 더 잘 표현하게 되며 단어들끼리 서로 멀어집니다. 하지만 여전히 같은 문장의 단어 벡터들끼리의 거리는 전혀 다른 문장의 단어 벡터들보다는 가까이 위치합니다. 이는 BERT의 벡터 표현이 ELMo보다는 더 contextulaized 되었다는 의미입니다. BERT는 주변 단어의 의미를 포함하여 특정한 단어의 의미를 파악하기는 하지만, 같은 문장에 등장한 단어라고 꼭 유사한 의미를 갖는 것은 아니라는 것도 이해하고 있습니다.
한 발 더 나아가서 GPT-2는 같은 문장 내의 단어 벡터는 더 이상 임의의 두 단어 벡터간의 유사도보다도 높지 않습니다. 위 그래프에서 알 수 있듯이 GPT-2의 intra-sentence similarity는 거의 모든 레이어에서 0에 가깝고, 오히려 첫 번째 레이어에서 그 값이 가장 큽니다. Intra-sentence similarity의 값이 평균적으로 0.2 보다 큰 BERT와 ELMo와는 다른 경향을 보입니다. 앞서 BERT에서 언급했듯이 같은 문장에 있는 단어라고 해서 반드시 유사도가 높은 것은 아닙니다. GPT-2의 사례는 anisotropy와 다르게 높은 intra-sentence similarity는 contextualization의 내재된 특성은 아니라는 것을 의미합니다. 같은 문장의 단어는 서로 유사도가 높지 않아도 contextualization이 잘 이루어집니다.
Static vs. Contextualized
평균적으로 정적 임베딩으로는 단어의 contextualized representations의 5%도 설명하지 못합니다. MEV를 다시 떠올려보겠습니다. 이 지표는 어떤 모델의 특정 레이어에서 contextualized representations의 첫 번째 주성분이 전체 분산 중 차지하는 비율을 의미합니다. 이는 결국 static embedding이 contextualized representations을 얼마나 잘 대체할 수 있는지에 대한 상한을 제시합니다. Contextualized representations은 비등방성을 갖기 때문에 모든 단어에서 대부분의 분산은 하나의 벡터로 표현될 수 있습니다. 다음 그래프는 균일 분포에서 추출한 임의의 단어에 대하여 anisotropy가 조정된 MEV 값의 평균을 나타냅니다.
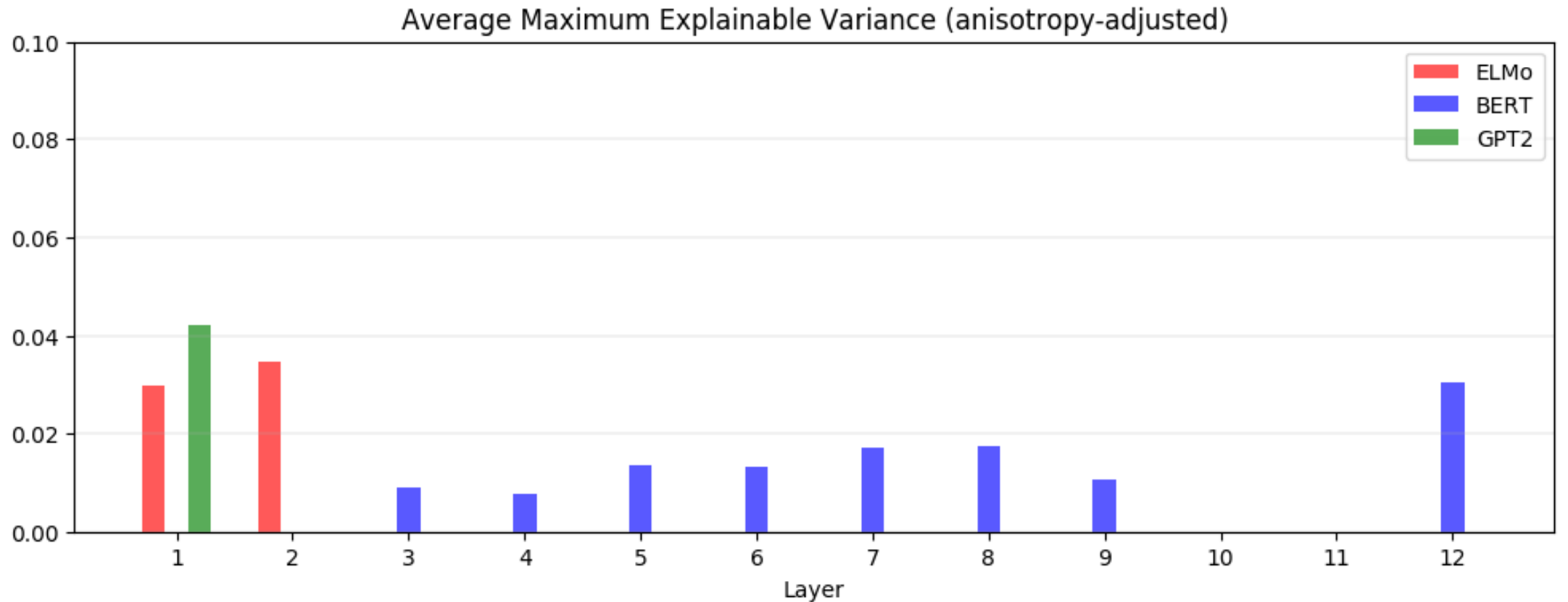
ELMo, BERT, GPT-2의 모든 레이어에서 5% 이상의 값을 갖지 않습니다. 5%라는 임계점은 최선의 경우를 의미한다는 것을 생각하면, GloVe의 정적 임베딩과 MEV가 최대가 되게 하는 정적 임베딩이 서로 비슷할 것이라는 점이 이론적으로 전혀 보장되지 않습니다.
하위 레이어의 contextualized representations의 주성분을 사용한 임베딩은 여러 벤치마크에서 GloVe나 FastText의 성능을 압도합니다. 다음 표를 통해 이를 확인할 수 있습니다. 문장 유사도 측정, 유추, concept categorization 등 여러 태스크에서 성능을 비교하였습니다.
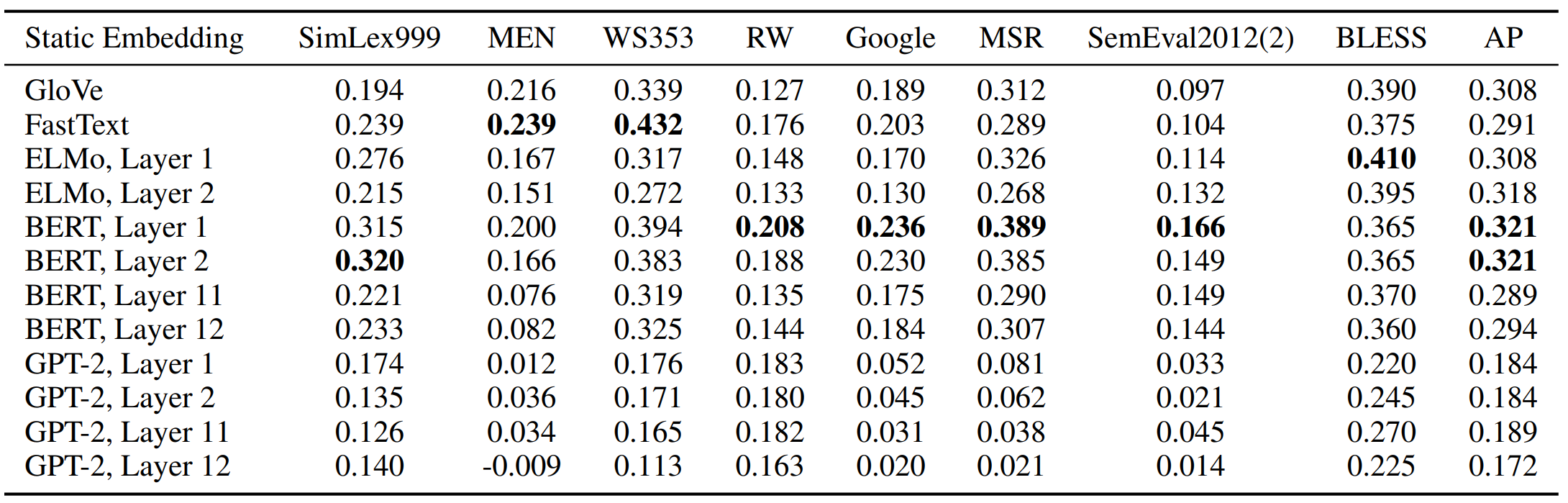
여기서 또 한가지 주목할 점은 오히려 상위 레이어의 단어 벡터의 주성분을 사용한 정적 임베딩이 하위 레이어보다 성능이 좋지 못하다는 점입니다. 이를 통해 일부 전통적인 벤치마크에서는 더 많이 context-specific한 벡터가 그리 효과적이지는 못함을 의미합니다.
Conclusion
정적 임베딩에서 등방성이 가져다주는 장점을 생각해보면 contextualized representations에서도 등방성은 장점이라고 생각할 수 있습니다. 물론 비등방성을 가짐에도 불구하고 정적 임베딩보다 매우 뛰어난 성능을 보여주기는 하지만, 등방성을 고려한 연구는 충분히 가치있을 것입니다. 저자는 anisotropy penalty를 부여하는 방식을 사용하면 훨씬 더 좋은 성능을 갖는 임베딩을 구현할 수 있을 것이라고 제안합니다.
또 한가지는 contextualized representations을 활용한 정적 임베딩 생성입니다. 메모리나 실행 시간을 고려하면 거대한 언어 모델에서는 contextualized representations 사용하기 어려울 때가 있습니다. 반면에 정적 임베딩을 사용한 모델인 배포가 훨씬 더 용이합니다. 연구 내용에서 contextualized representations의 첫 번째 주성분을 사용한 정적 임베딩이 이미 GloVe나 FastText 같은 정적 임베딩의 성능을 넘어섰다는 점에서 의미있는 시도로 보여집니다.
Further Thinking
새롭게 알게 된 내용이 정말 많은 논문이었고, 그 안에서도 요하는 배경지식이 매우 많은 논문이었습니다. 아는 게 많지 않아서 논문 하나를 읽으면서도 정말 많이 찾아본 것 같은데, 그 깊이가 깊지 않아서 이해하지 못한 부분이 여전히 남아있는 것 같습니다. 먼저 단어에 대한 벡터 표현이 레이어마다 달라진다는 점이 조금 어려웠습니다. 학습 데이터가 모델의 마지막 레이어에 이르러야 역전파가 이루어질 것인데, 레이어마다 다른 벡터 표현을 갖는다는 것은 각 레이어를 지날 때마다 가중치가 갱신된다는 의미인지, 아니면 순전파가 끝나고 역전파가 레이어별로 이루어질 때마다 그 가중치를 저장해서 각 단어의 벡터 표현을 계산한다는 의미인지를 명확하게 이해하지 못했습니다.
또 이와 비슷한 맥락에서 BERT와 같이 contextualized representations을 사용한 모델도 임베딩 레이어는 존재하게 되는데, 그렇다면 토큰화된 단어가 임베딩을 통과할 때, 서로 다른 맥락에서 유래한 단어가 서로 다른 벡터에 매핑된다는 것인지, 아니면 일단 같은 벡터에 매핑된 후, 모델의 각 레이어를 거치면서 서로 다른 길을 간다는 것인지에 대한 개념이 명확하지 않습니다. 만약 후자라면, 첫 번째 의문점과 연결되어 각 레이어에서 같은 문장의 다른 단어와의 관계를 비교하며 임베딩된 벡터를 조금씩 수정해나간다는 의미일텐데, 이러한 이해가 맞는지에 대해서 추가적으로 공부해봐야할 것 같습니다.




댓글