
이전에 리뷰했던 논문 How Contextual are Contextualized Word Representations? Comparing the Geometry of BERT, ELMo, and GPT-2 Embeddings에는 정적 임베딩을 사용하는 경우 벡터가 등방성을 가질 경우 성능이 더욱 좋다는 내용이 있었습니다. 이것이 어떤 의미를 갖는지 궁금해서 해당 내용을 다룬 논문인 All-but-the-Top: Simple and Effective Postprocessing for Word Representations를 읽어보았습니다. 번역을 통해 오히려 이해가 어려워지거나, 원문의 표현을 사용하는 게 원래 의미를 온전히 잘 전달할 것이라고 생각하는 표현은 원문의 표기를 따랐습니다. 오개념이나 오탈자가 있다면 댓글로 지적해주세요. 설명이 부족한 부분에 대해서도 말씀해주시면 본문을 수정하겠습니다.
1. Overview
단어와 단어 간의 상호작용은 자연어의 기본 단위입니다. 단어는 개별적인 원자 단위로 쉽게 모델링할 수 있지만, 이를 통해서 단어 사이의 관계를 파악하는 것은 불가능합니다. word2vec이나 GloVe와 같은 당시로써는 최신의 단어의 분산 표현(distributional representations) 개념은 텍스트 분류, 기계 번역, 지식 베이스 완성(knowledge base completion) 여러 NLP의 응용분야의 판도를 바꿔놓았습니다. 이는 효과적으로 언어적 규칙성(linguistic regularities)를 포착하는 표현의 기하적 특징에서 덕분이었습니다. 단어의 의미적 유사성은 각 단어에 대응하는 벡터 표현의 유사성에 의해 잘 포착되었기 때문입니다.
당시에는 단어의 표현을 잘 이해하기 위한 다양한 방법이 제시되었습니다. 예를 들어 Collobert, Turian의 연구에서는 언어 모델과 다운스트림 태스크를 함께 학습하는 자기 지도 학습법으로 단어의 벡터 표현을 학습합니다. 단어의 표현을 유도하는 알고리즘은 서로 큰 차이를 가짐에도 불구하고, 다양한 내재적 또는 외재적 평가 테스트베드에서 성능은 거의 비슷합니다. 이 논문에서 저자는 간단한 처리를 통해 기존에 존재하는 벡터 표현의 성능을 향상시키는 방법을 발견하였습니다. 제안된 알고리즘은 다음과 같은 관찰 결과에서 영감을 받았습니다.
Observation
저자가 실험한 모든 벡터 표현은 많은 언어에서 다음과 같은 속성을 갖습니다.
- 단어의 벡터 표현의 평균은 0이 아닙니다. 실제로 단어 벡터는 거대한 공통 벡터를 공유합니다. 이 공통 벡터의 노름(norm)은 단어 벡터의 평균 노름의 최대 절반까지 차지하기도 합니다.
- 공통 평균 벡터(common mean vector)를 제거하면 벡터 표현은 등방성(isotropic)과는 거리가 멀어집니다. 실제로 대부분의 단어 벡터에서 많은 에너지는 매우 낮은 차원의 부분 공간에 존재합니다. (예를 들어서 300차원 중 8차원)
Implication
모든 단어가 같은 공통 벡터를 공유하고 같은 주요 dominating directions(많은 정보를 갖는 특정 차원)을 갖고, 그러한 벡터와 directions는 단어의 벡터 표현에 같은 방식으로 큰 영향을 미치기 때문에, 저자는 다음과 같은 방법으로 이들을 제거하였습니다. (a) 모든 단어 벡터에서 0이 아닌 평균 벡터(nonzero mean vector)를 제거하여 효과적으로 에너지를 줄입니다. 논문에서 에너지는 벡터의 주성분이 설명하는 분산의 비율을 의미하는데, 쉽게는 특정 방향이나 차원의 벡터가 갖는 정보의 양이라고 생각하면 될 것 같습니다. (b) 벡터 표현을 dominating D directions에서 멀어지게 투영함으로써효과적으로 차원을 줄입니다. 실험을 통해 D는 벡터 표현의 차원, 학습 방법과 특정 하이퍼파라미터, 학습 말뭉치와 같은 벡터 표현과 다운스트림 태스크에 의존한다는 것을 확인하였습니다. 그럼에도 불구하고, 경험적으로 D의 값을 d/100으로 결정하면 다양한 언어, 벡터 표현, 테스트 시나리오에서 대부분 잘 맞습니다. 여기서 d는 단어 표현의 차원을 의미합니다.
저자가 제안하는 후처리(postprocessing)은 사실 직관과는 잘 맞지 않습니다. 일반적으로는 주요한(dominant) 성분보다는 약한 방향(weakest directions)의 벡터를 제거하여 차원을 축소합니다. 하지만 이러한 후처리는 실험에서 확인할 수 있듯이 단어 표현이 더욱 정제되고(purified) 등방성을 갖게 (isotropic)합니다.
Experiments
공통 부분을 제거하여 단어를 후처리함으로써저자는 처리된 단어 표현이 언어의 규칙성을 더욱 잘 포착함을 발견하였습니다. 저자는 원래의 단어 표현과 처리된 단어 표현을 세 가지 표준적인 어휘 수준(canocical lexical-level)의 태스크에서 비교하며 이 효과를 정량적으로 입증합니다.
- 단어 유사도(word similarity) 태스크는 벡터 표현이 두 단어 사이의 유사도를 어느 정도로 파악하는지를 시험합니다. 처리된 표현이 일곱 개의 서로 다른 데이터셋에서 평균적으로 1.7% 정도로 일관되게 우수한 성능을 보였습니다.
- 분류(concept categorization) 태스크는 단어 표현의 클러스터가 단어의 의미론적으로 얼마나 이해하는지를 시험합니다. 처리된 표현은 세 개의 데이터셋에서 2.8%, 4.5%, 4.3%로 일관되게 뛰어난 성능을 보였습니다.
- 단어 유추(word analogy) 태스크에서는 두 표현이 잠재적인 언어적 관계를 얼마나 잘 파악하는지를 시험합니다. 성능은 의미 유추(semantic analogies)에서 0.5%, 구문 유추(syntactic analogies)에서 0.2%, 최종적으로 0.4%만큼 향상되었습니다. 저자는 유추를 풀이하는 과정 중 뺄셈에 의해 주요한 성분중 일부가 제거되었기 때문에 성능 향상이 이전 태스크처럼 큰 폭을 보이지 않는다고 생각하였습니다.
외재적 평가(extrinsic evaluation)은 특정한 다운스트림 태스크에서 표현의 효과를 평가합니다. 저자는 semantic textual similarity와 같이 문장을 모델링하는 표준화되고 중요한 외재적 평가 태스크에서 후처리의 효과를 평가합니다.여기서 저자는 문장을 문장의 단어 벡터들의 평균으로 나타내고 문장 간의 코사인 유사도를 비교합니다. 후처리 결과 성능은 21개의 서로 다른 데이터셋에서 일관되게, 평균적으로 4% 정도 향상되었습니다.
단어 표현은 특히 신경망 아키텍처와 함께 지도 학습과 관련된 NLP 태스크에서 특히 성공적이었습니다. 실제로 저자는 잘 설계된 CNN 분류기와 세 개의 RNN 분류기(RNN, GRU, LSTM)을 사용하는 표준적인 텍스트 분류 태스크에서 후처리의 효과를 확인하였습니다. 두 개의 서로 다른 사전 학습된 단어 벡터, 다섯 개의 데이터셋과 네 개의 다른 아키텍처에서 후처리는 대부분의 경우 평균 2.85% 정도로 향상된 성능을 보였습니다.
Related Work
이 논문은 앞서 언급한 word2vec, GloVe와 같이 단어 표현 알고리즘과 직접적인 연관이 있습니다.
기존 연구에서도 이 논문의 연구와 같은 후처리를 적용하는 사례가 있었지만, nulling directions를 선택하는 방법이 근본적으로 다릅니다. Arora의 연구에서는 첫 번째 dominating vector가 데이터셋에 특화(dataset-specific)되었습니다. Arora의 연구에서 먼저 문장의 표현을 모든 semantic textual similarity 데이터셋에서 계산하고, top direction을 문장 표현에서 추출한 후 최종적으로 그 방향에서 멀어지게 투영하였습니다. 이렇게 함으로써 top direction은 전체 데이터셋에서 공통적인 정보를 내재적으로 인코딩하게 되며, headlines 데이터셋에서 top direction은 뉴스 기사를 인코딩할 것이며, Twitter 15 데이터셋의 top direction은 트윗의 공통된 정보를 인코딩할 것입니다. 반대로 이 연구에서는 dominating vectors가 전체 어휘에 대해서 인코딩됩니다.
조금 더 일반적으로는 가장 중요한 주성분(top principal components)를 제거하는 아이디어는 positive-valued, high-dimensional data matrix analysis에서 연구되었습니다. Bullinaria와 Levy는 cooccurence matrix에서 가장 큰 분산을 갖는 성분이 어휘 의미가 아닌 정보에 의해 손상되었음을 가정하고, 휴리스틱하게 top principal components를 제거하는 것을 정당화합니다. 모든 엔트리가 양의 값을 갖는 Price의 population matrix analysis에서도 비슷한 아이디어가 나타납니다. 반면 논문의 후처리 연산은 양과 음의 값을 모두 갖는 밀집 저차원 분산 표현에 대한 것입니다.
저자는 후처리 연산이 벡터 표현이 등방성을 가져 self-normalization properties가 더욱 강해지게 한다고 가정합니다. 요점은 이 등방성 조건을 명시적으로 적용하여 새로운 임베딩 알고리즘을 만들 수 있다는 것입니다.
2. Postprocessing
저자는 다음과 같이 공식적으로 사용할 수 있는 네 가지 단어 표현에 대하여 관찰 결과를 실험하였습니다. 사용한 단어 표현은 Google News로 학습된 Word2Vec, Common Crawl로 학습된 GloVe, Wikipedia와 TSCCA로 학습된 RAND-WALK, 2010 Wikipedia 말뭉치로 CBOW와 Skip-gram 방식으로 학습된 벡터 표현입니다. 각 representations에 대한 자세한 내용은 다음 표와 같습니다.

여기서 v(w)∈Rd를 어휘사전(vocabulary) V 안에서 주어진 단어 w에 대한 단어 표현이라고 하겠습니다. 저자는 다음과 같이 위에서 언급한 표현들에 대해 두 가지 현상을 발견하였습니다.
- v(w):w∈V의 평균은 0이 아닙니다. 모든 v(w)가 0이 아닌 공통 벡터를 공유하여μv(w)=˜v(w)+μ와 같이 나타낼 수 있습니다. 여기서 μ는 모든 v(w)의 평균이며 수식으로는 μ=1/|V|∑w∈Vv(w) 와 같이 나타냅니다. 위 표의 마지막 두 열에서 확인할 수 있듯이 μ의 노름은 모든 v(w)의 노름의 평균의 대략 1/6에서 1/2 정도가 됩니다.
- ˜v(w):w∈V는 등방성을 갖지 않습니다. u1,…,ud를 주성분 분석(PCA)에 의해 복원된 ˜v(w):w∈V의 주성분이라고 하고, σ1,…,σd를 각각에 대응하는 정규화된 분산 비율(normalized variance ratio)라고 하겠습니다. 각 ˜v(w)는 다음과 ˜v(w)=∑di=1αi(w)ui와 같이 u의 선형 결합으로 표현될 수 있습니다. 아래 그래프에서 볼 수 있듯이 σi가 지수적으로 감쇠하다가 나중에는 어떤 상수처럼 되어버립니다. 이는 모든 i≤D에 대해 αi≫αj와 j≫D를 만족하는 D가 존재함을 의미합니다. 그림에서 D가 대략 d=300일 때, 10임을 알 수 있습니다.

여기서 α는 뒤에서 설명되겠지만 PCA를 수행한 이후 계산된 주성분을 의미합니다. 예를 들어 α1은 첫 번째 주성분을 의미합니다. 즉 앞서 언급한 식에서 D보다 작은 i번째 인덱스에 해당하는 α가 D보다 큰 j번째 인덱스에 해당하는 모든 α보다 훨씬 더 크게 하는 D 값이 존재함을 의미합니다. 그리고 위 그림에서는 그 값이 10정도인 것을 알 수 있습니다. 실제로 10을 기준으로 이전의 값은 높은 variance ratio를 갖고, 이후의 값은 거의 어떤 작은 상수에 수렴하는 것처럼 보입니다.
Angular Asymmetry of Representations
단어의 벡터표현에는 word2vec이나 GloVe를 포함한 PMI-based와 CCA-based spectral factorization 방법이 있습니다. 여기서 PMI는 Pointwise Mutual Information을 의미하여 PMI-based 방법은 단어 쌍 사이의 PMI를 나타내는 항목이 있는 행렬을 구성합니다. 이는 두 단어의 PMI가 의미적 연관성을 포착한다는 것을 전제로 합니다. 즉 유사한 문맥에서 자주 함께 등장하는 단어들은 높은 PMI 값을 가질 것입니다. 그 후 spectoral factorization이 PMI 행렬에 적용되어 밀집 임베딩(dense word embeddings)으로 변환됩니다. CCA는 Canocial Correlation Analysis를 의미하여 변환된 변수 간의 상관관계가 최대가 되는 두 변수 집합의 선형 변환을 찾는 위한 방법입니다. 단어 임베딩을 생성할 때 CCA는 서로 다른 소스의 word-context 행렬 또는 서로 다른 방식으로 구성된 데이터처럼 두 가지 방법으로 적용하여 공통된 임베딩 공간을 찾을 수 있습니다. 이 방식을 통해 변환된 공간에서 두 가지 방법의 상관 관계를 최대화하여 단어와 문맥에 대한 임베딩을 도출하고, 공유되는 의미 정보를 캡처하는 단어 벡터로 이어집니다. CCA-based spectral factorization 방법은 생성 모델과 같이 오랫동안 확률론적 관점에서 이해되어 왔으며 당시에는 NLP에서 PMI-based 방법에 대한 연구 노력에 대응하여 뒤늦게 연구가 수행되었습니다.
Arora는 RAND-WALK로 알려진 모든 단어는 d-차원의 벡터로 파라미터화하는 문장의 생성 모델을 제안하였습니다. 단어 벡터는 등방성을 갖는다는 핵심적인 가정을 통해 PMI 기반 단어 표현 방법들은 최대 가능도 규칙(maximum likelihood rule)의 관점에서 RAND-WALK 모델에 따라 설명할 수 있습니다. 저자는 PMI 기반 방법을 통해 학습된 벡터의 평균이 0도 아니고 등방성을 갖지도 않는다는 관찰을 통해 이 가정에 위배됨을 발견하였습니다.
이러한 모순은 관찰된 스펙트럼 속성(observec spectral properties)과 맞도록 단어 벡터에 대한 제약을 완화함으로써 해결됩니다. 완화 조건은 단어 벡터가 원점까지의 거리가 단어 벡터의 평균 노름의 일부인, 저차원 하위 공간에 있는 점을 중심으로 등방성을 가져야 한다는 것입니다. 논문의 주요 결과는 이렇게 확장된 매개변수 공간에서도 최대 가능도 규칙이 PMI-based spectral factorization 방법과 계속 연관된다는 것을 보여줍니다.
2.1 Algorithm
모든 단어 벡턱 공통 벡터 μ를 공유하고 같은 dominating directions을 가지며, 이 벡터와 directions는 단어 표현에 큰 영향을 주기 때문에, 저자는 이를 제거하기로 하였습니다. 이 과정은 다음과 같습니다.
Algorithm 1
단어 표현에 대한 후처리 알고리즘
Input : 단어 표현 v(w),w∈V, 임계(threshold) 파라미터 D
- v(w),w∈V의 평균을 계산합니다: μ←1|V|∑w∈Vv(w), ˜v(w)←v(w)−μ
- 주성분(PCA components)를 계산합니다: u1,…,ud←PCA(˜v(w),w∈V)
- 표현(representations)을 처리합니다: v′(w)←˜v(w)−∑Di=1(u⊺iv(w))ui
Output: 후처리된 표현 v′(w)
Significance of Nulled Vectors
단어의 표현이 1≤ℓ≤D에 대하여 top D개의 PCA 계수(coefficients) αℓ(w)의 항으로 표현된다고 생각하겠습니다. 저자는 이 몇 개의 계수가 단어의 빈도(frequency)를 잘 인코딩한다는 것을 발견하였습니다. 아래 그림은 (α1(w),α2(w))와 유니그램 확률(unigram probability) p(w)의 기하학적 상관관계를 보여줍니다.
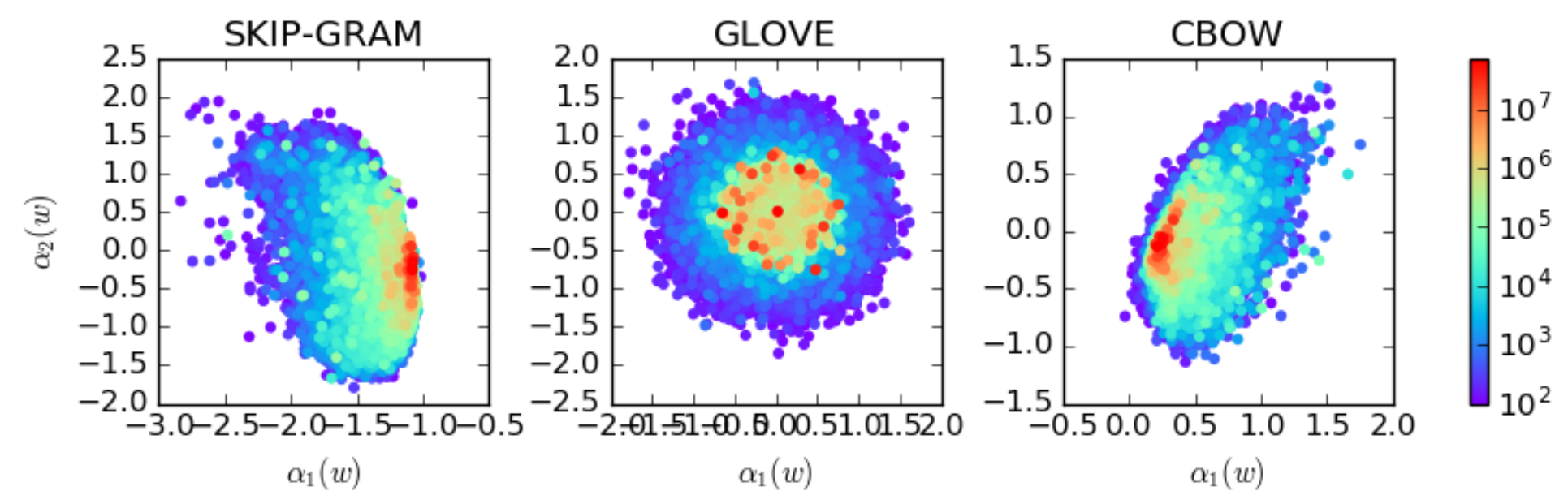
Discussion
논문에서 제안한 처리 알고리즘에서 제거(nulled)될 성분의 개수인 D는 튜닝이 필요한 유일한 하이퍼파라미터입니다. 경험에 의하여 D는 d/100으로 결정하는 것이 좋다는 것을 확인하였습니다. 여기서 d는 단어 벡터의 차원입니다. d=300이 발표된 단어 벡터들에서 표준으로 사용되었기 때문에 이 값을 사용하였습니다.
2.2 Postprocessing as a “Rounding” towards isotropy
등방성에 대한 아이디어는 Arora의 논문의 분배 함수(partition function)에서 유래하였습니다.
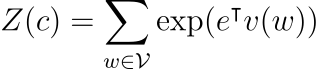
여기서 Z(c)는 모든 단위 벡터 c에 대해 근사적으로 상수여야 합니다. 따라서 저자는 다음과 같이 수학적으로 등방성을 측정하였습니다. 즉 어떤 단위 벡터가 입력으로 주어지든 대략 어떤 상수에 가까운 결과가 출력되어야 합니다.
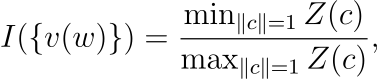
여기서 I(v(w)는 0에서 1 사이의 값이며, I(v(w)가 1에 가깝다는 것은 v(w)가 더욱 isotropic(등방성을 가짐)하다는 것을 의미합니다. 즉 I(v(w)→1이 되도록 후처리 알고리즘이 고안되었습니다.
V를 모든 단어 벡터를 쌓은 행렬이라고 하면, 각 행은 단어 벡터에 해당합니다. 1|V|을 모든 원소가 1인 |V|-차원의 벡터라고 하면, Z(c)는 다음과 같이 나타낼 수 있습니다.
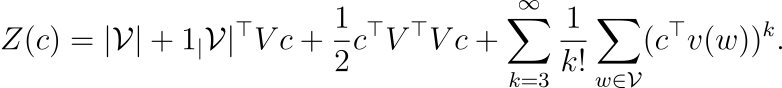
따라서 I(v(w)는 매우 거칠게(coarsely) 다음과 같이 근사될 수 있습니다.
- 일차 근사(A first order approximation)
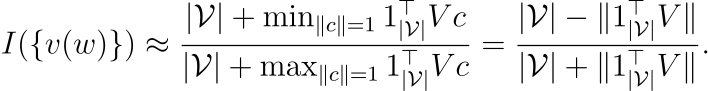
I(v(w)=1이라고 하면, |1⊺|V|V|=0이 되고, 이는 ∑w∈Vv(w)=0과 같습니다. 일차 근사는 제안된 알고리즘의 첫 번째 단계인 v(w)의 평균을 0으로 만드는 것과 일치합니다.
- 이차 근사(A second order approximation)

σmin과 σmax는 각각 차례대로 V의 최솟값과 최댓값입니다. I(v(w)=1이라고 하면, |1⊺|V|V|=0이 되고, σmin=σmax가 됩니다. σmin=σmax는 v(w)의 스펙트럼이 평평(flat)해야 함을 의미합니다. 제안된 알고리즘의 두 번째 단계는 가장 큰 특이값(singular values)를 제거하고 V의 스펙트럼을 명시적으로 납작하게(flatten) 만듭니다.
Empirical Verification
저자는 실험을 통해 I(v(w)를 후처리하는 것의 효과를 검증하였습니다. \argmax|c|=1Z(c) 또는 \argmin|c|=1Z(c)의 closed-form solution(반복적인 검증이나 계산 없이 구할 수 있는 해)가 없고, 모든 c에 대하여 일일히 계산할 수 없기 때문에, 다음 공식을 사용합니다.
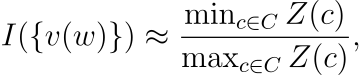
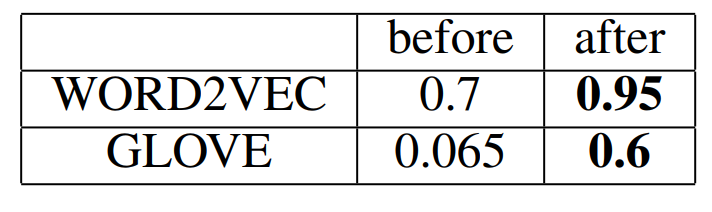
C는 V⊺V의 고유벡터(eigenvector)이며 원랴의 벡터와 후처리된 벡터에 대한 I(v(w)의 값은 아래 표에서 확인할 수 있습니다. 처리 결과 등방성을 띄는 정도가 상당히 증가한 것을 확인할 수 있습니다.
Isotropy property(등방성을 띄는 속성)을 확인하는 공식적인 방법은 Z(c)의 값이 c와 독립적으로 상수인지를 확인하는 것처럼, self-normalization 속성을 확인하는 것입니다. 아래 그래프를 통해 임의추출한 1000개의 c에 대해서 이 방법을 사용한 검증 결과를 확인할 수 있습니다.
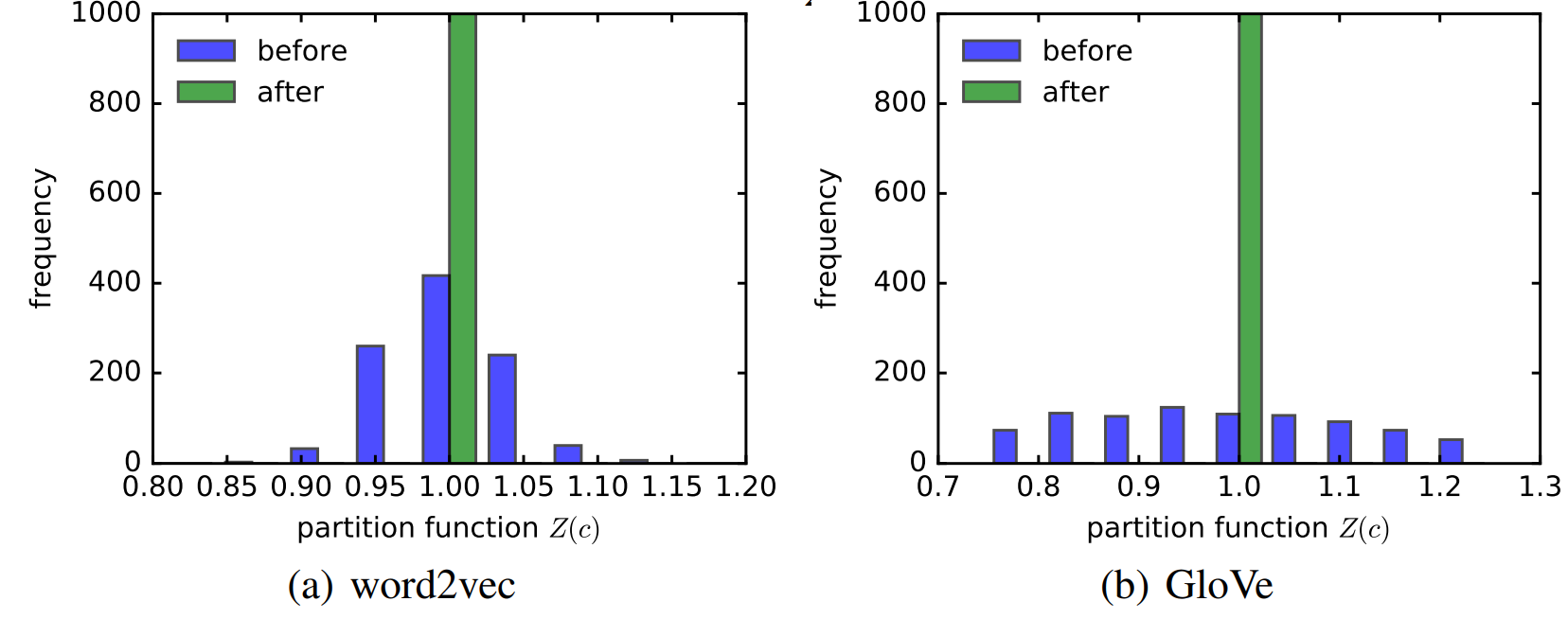
3. Experiments
실험에서는 널리 사용되는 Word2Vec과 GloVe의 사전학습된 단어의 벡터 표현을 사용하였습니다. Word2Vec에는 D=3을 사용하였고, GloVe에는 D=2를 사용하였습니다. 유사한 단어는 유사한 표현을 갖는다는 것을 핵심 전제로 하였습니다. 단어 표현을 검증하는 전통에 따라 세 가지 표준적인 어휘 단계 태스크(lexical-level tasks)인 단어 유사도(word similarity), 개념 분류(concept categorization), 유추(word analogy)와 하나의 문장 단계 태스크인 semantic textual similarity를 사용하였습니다. 후처리된 표현은 세 가지 태스크 모두에서 일관적으로 향상된 성능을 보였고, 처음 두 개의 태스크에서 특히 눈에 띄게 성능이 개선되었습니다.
Word Similarity
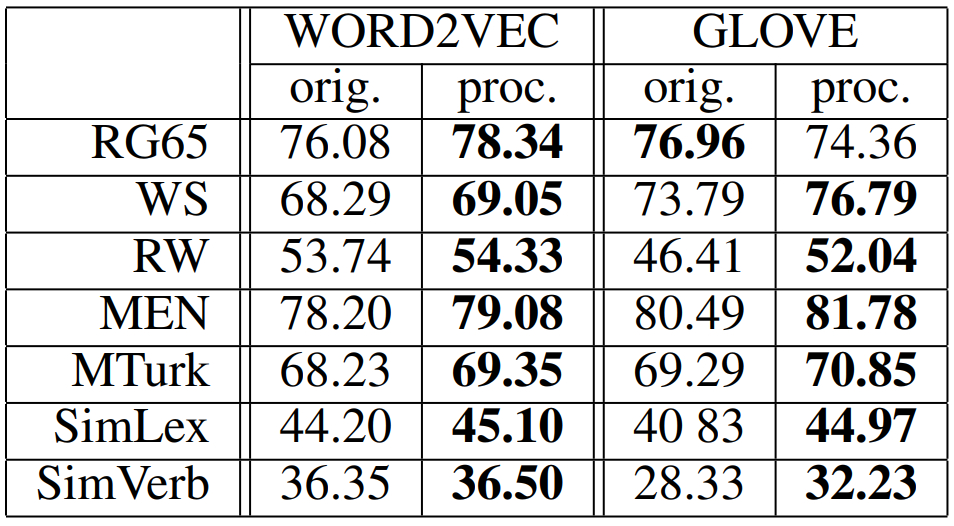
단어 유사도 태스크는 단어 쌍이 주어지면 알고리즘이 유사도 점수를 할당합니다. 단어 쌍의 유사도가 높으면 점수가 높고 아니면 그 반대입니다. 알고리즘은 사람의 판단(human judgement)와 비교한 Spearman’s rank correlation으로 평가됩니다.
다음은 실험에 사용한 7개의 데이터셋에 대한 점수를 나타낸 표입니다. 실험에서 유사도를 측정하는 데는 코사인 유사도를 사용하였습니다. 이 결과를 통해 단어 표현의 공통된 부분을 제거하면 남은 단어 표현이 의미 관계나 유사성을 더욱 잘 파악한다는 것을 알 수 있습니다.
Concept Categorization
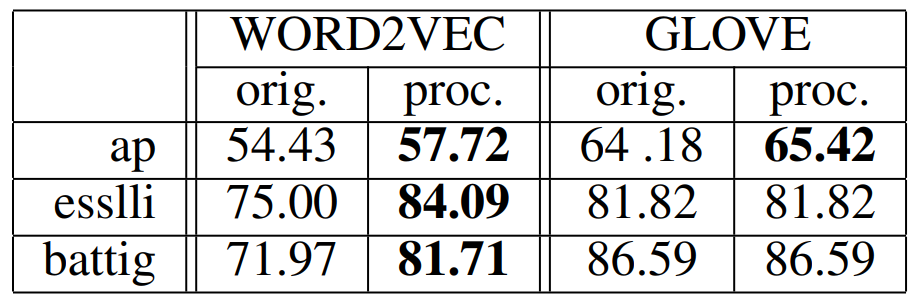
이 태스크는 어떤 개념의 집합(set of concepts)이 주어지면 알고리즘이 이들을 서로 다른 카테고리로 분류하는 것을 통해 간접적으로 유사도를 측정합니다. 예를 들어 곰과 고양이는 모두 동물이며, 도시와 나라는 둘다 구역(district)과 관계가 있습니다. 군집화가 잘 이루어졌는지는 전체 개체 중 올바르게 분류된 개수를 계산하는 purity를 사용하여 측정합니다.
이 실험에는 세 개의 데이터셋을 사용하였습니다. 군집화(clustering)에는 전통적인 방법인 k-Means 알고리즘을 사용하였습니다.
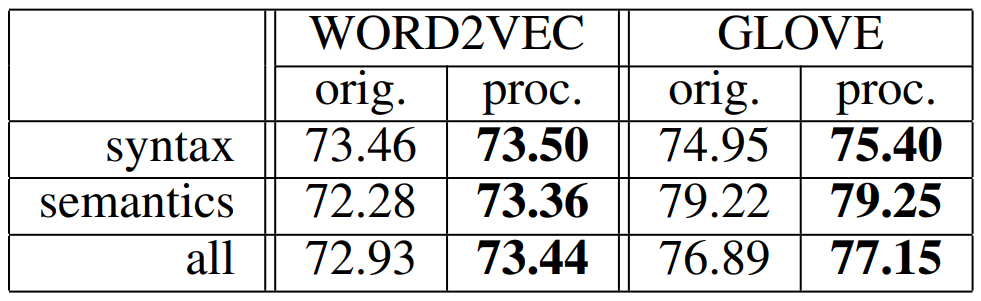
Word Analogy
이 태스크는 단어 표현이 잠재적인 언어학적 관계를 이해하는지를 확인합니다. w1,w2,w3 세 개의 단어가 주어졌을 때, 유추 태스크에서는 w2와 w1의 관계를 보고 w3에 대응하는 w4를 찾습니다. w4는 v(w4)와 v(w2)−v(w1)+v(w3)의 코사인 유사도를 최대로 하는 단어입니다. 아래 결과를 통해 후처리가 이 태스크에서도 성능을 약간 개선하지만, 앞의 태스크만큼은 아닌 것을 볼 수 있습니다. 저자는 v(w2)에서 v(w1)를 뺄 때, dominant components가 제거되기 때문에 후처리의 효과가 감소한다고 생각하였습니다.
Semantic Textual Similarity
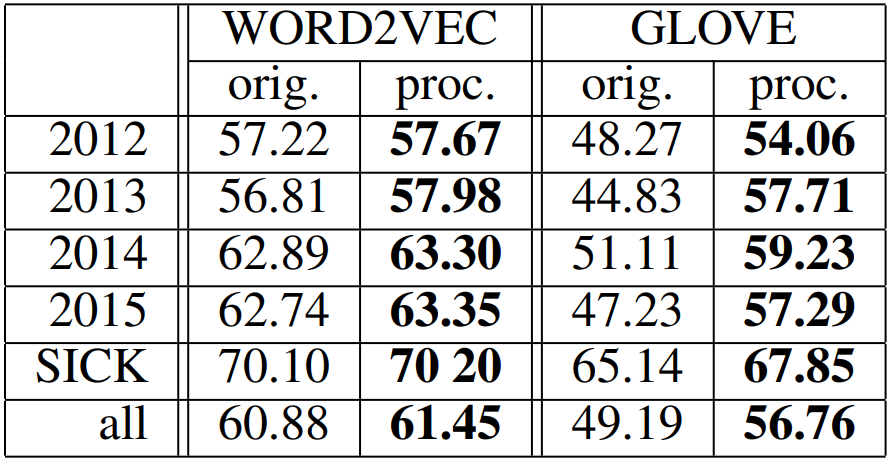
외재적 평가(extrinsic evaluation)은 단어 표현이 특정 다운스트림 태스크에 미치는 영향을 측정합니다. 여기서는 알고리즘이 두 문장 사이의 의미 관계를 파악할 수 있는지를 확인하기 위해 표준적인 문장 모델링 태스크인 STS에서 후처리의 영향을 분석하였습니다. 각 문장 쌍에 대하여 알고리즘은 유사도를 측정해야 합니다. 여기서는 총 20개의 데이터셋을 사용하였습니다.
문장에 포함되는 단어 벡터의 평균을 통해 문장 벡터를 나타내는 방법은 의미 정보를 인코딩하는 효과적인 방법입니다. 논문에서도 이 방식을 사용하여 문장 s의 벡터 표현을 v(s)=1|s|∑w∈sv(w)와 같이 나타냅니다. 다음 표를 통해 일관적으로 성능이 개선되었음을 확인할 수 있습니다.
4. Postprocessing and Supervised Classification
논문이 쓰인 당시 지도 학습을 사용하는 NLP 다운스트림 태스크에서는 신경망의 학습 능력과 단어 표현을 결합하여 성능이 크게 향상되었습니다. 저자는 다양한 신경망 아키텍처의 성능을 감성 분석 태스크를 통해 평가하였습니다. 문장이 주어지면 알고리즘은 이 문장이 어느 카테고리에 속하는지를 결정해야 합니다. 이진 분류 문제라면 긍정, 부정을 분류하고, 조금 더 세밀하게 분류해야 한다면 매우 긍정, 긍정, 중립, 부정, 매우 부정의 다섯 개의 카테고리로 분류합니다.
저자는 네 개의 서로 다른 신경망 아키텍처인 CNN, RNN, GRU, LSTM을 다섯 개의 벤치마크에서 평가하였습니다. 평가 결과는 아래와 같습니다. 후처리 결과 40개의 실험 중 34개로 대부분의 실험에서 평균적으로 2.32% 만큼의 성능 향상을 보였고, 나머지 실험에서도 성능은 거의 비슷합니다.

저자는 더 많은 다운스트림 태스크에서 후처리의 효과를 검증하는 것도 의미가 있을 것이라고 생각하였고 향후 저자 뿐만 아니라 여러 연구 단체에서 이를 검증하기를 기대합니다.
Discussion
피드포워드부터 재귀(RNN, GRU, LSTM 중 어느 것이든)까지 모든 신경망 아키텍처는 은닉 상태, 또는 입력에 대한 하나의 선형 변환을 포함합니다. 따라서 논문에서 제안한 후처리 작업은 원칙적으로 신경망에 의해 자동으로 학습될 수도 있습니다. 하지만 이는 학습 과정과 학습 데이터에 의존합니다. 만약 학습 예제와 훈련 프로세스가 이 후처리 작업의 의미를 잘 살린다면 학습할 것이고, 그렇지 않다면 학습이 되지 않을 것입니다. 하지만 이는 최적화(SGD) 과정이나 샘플 노이즈의 한계로 인해서 실제로는 매우 어렵습니다.
5. Conclusion
논문에서는 단어의 벡터 표현이 더욱 뛰어난 성능을 갖게 하는 후처리 작업을 제안하였습니다. 후처리는 모든 단어에서 가장 중요한 주성분을 제거하는 것으로 이루어집니다. 이런 간단한 작업은 다운스트림 태스크에서 단어 임베딩이나 태스크에 특화된 임베딩을 초기화하는데 사용할 수 있습니다. 논문에서는 주로 사용되는 Word2Vec과 GloVe를 실험하였고, 영어를 사용하였지만, 추가적인 실험을 통해서 제안한 후처리 작업이 다른 언어에서도 여전히 효과적임을 검증하였습니다.
6. Further Thinking
Appendix에 저자가 전달하고 싶은 내용이 많이 남아 있지만, 아직은 다 확인하지 못하였습니다. 이 부분에 대해서 조금 더 자세히 읽어봐야할 것 같습니다. 특히 논문에서 제안한 후처리가 신경망 아키텍처에서 내재적으로 학습될 수도 있다는 부분을 탐구한 내용이 흥미로워보였습니다. 이 부분에 대해서 조금 더 고민해보고 추후 본문을 수정할 예정입니다. 이 논문 역시 지금껏 임베딩을 다룬 논문이 모두 그랬듯이 많은 복잡한 수식을 포함하고 있습니다. NLP 문제를 딥러닝으로 풀 수 있게 된 이유가 결국 단어를 숫자로 표현할 수 있었기 때문인데, 이 표현을 효과적으로 생성하기 위한 연구라서 그런지 정말 복잡하고 참신한 수식이 많이 등장하는 것 같습니다. 계속해서 이와 관련해서 공부해서 NLP의 기원에 대해서 더 알아보고 싶다는 생각이 들었습니다.




댓글